Dicas de Conversões Angulares para a Topografia
A topografia é uma ciência que lida com a medição e representação da superfície terrestre. Uma parte essencial dessa disciplina envolve as medições angulares, fundamentais para determinar e calcular as direções, posições, distâncias e desníveis no terreno.
Compreender as definições e cálculos de ângulos é essencial para agrimensores. A aplicação correta desses conceitos permite a reconstituição precisa de memoriais descritivos e a interpretação de plantas topográficas, que são usadas para representações de terrenos, planejamento de obras e resolução de questões jurídicas de propriedade.
Neste artigo, vamos explorar alguns conceitos essenciais de medições angulares e aplicações práticas de conversões de rumos para azimutes, bem como a transformação do sistema sexagesimal (graus, minutos e segundos) para graus decimais, com exemplos de cálculos no QGIS.
A Importância da Medição Precisa de Ângulos na Topografia
A medição precisa de ângulos é vital na topografia para garantir a exatidão na representação das áreas e na determinação de limites. Um erro angular pode gerar discrepâncias significativas em mapas, especialmente em grandes áreas. Esses dados afetam diretamente a criação de plantas topográficas, projetos de infraestrutura e demarcações de imóveis.
Como os Ângulos eram medidos no Passado?
Historicamente, os ângulos eram medidos usando instrumentos como o astrolábio , sextante e, mais tarde, o teodolito óptico. Esses métodos exigiam altos níveis de habilidade, e a precisão dependia muito da experiência do operador e da qualidade do equipamento.
Instrumentos utilizados Hoje para medir Ângulos
Atualmente, a estação total e os teodolitos eletrônicos dominam as medições angulares na topografia. Esses instrumentos utilizam tecnologia eletrônica avançada para oferecer medições extremamente precisas, com erros mínimos, mesmo em terrenos desafiadores.
O que é o Sistema Sexagesimal?
O sistema sexagesimal, que divide o círculo em 360 graus, cada grau em 60 minutos e cada minuto em 60 segundos, é amplamente utilizado para medir ângulos na topografia. Ele facilita a padronização e a interpretação dos dados, permitindo que topógrafos e engenheiros se comuniquem de maneira clara e eficiente.
Por exemplo, considere o seguinte valor:
45° 30′ 25″
A leitura desse valor seria: quarenta e cinco graus, trinta minutos e vinte e cinco segundos.
- Graus (°) indicam a maior unidade e variam de 0 a 360 em uma circunferência completa.
- Minutos (‘) são subdivisões dos graus, com 60 minutos compondo um grau.
- Segundos (“) são subdivisões dos minutos, com 60 segundos compondo um minuto.
Este valor pode ser usado em várias áreas, como topografia, astronomia e navegação, para expressar a medida de um ângulo ou a posição de um ponto na superfície terrestre através de coordenadas geodésicas (latitude e longitude).
Diferença entre Rumo e Azimute
Definição de Azimute
O azimute é o ângulo medido em relação ao norte, sempre no sentido horário, e pode variar de 0° a 360°. Ele é usado para determinar a direção precisa de um ponto a outro.
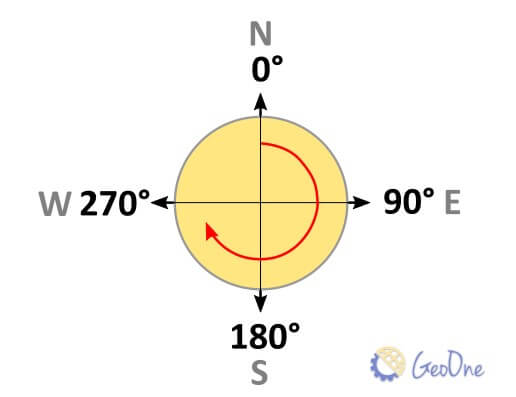
Confira aqui como calcular o azimute a partir das coordenadas entre dois pontos.
Definição de Rumo
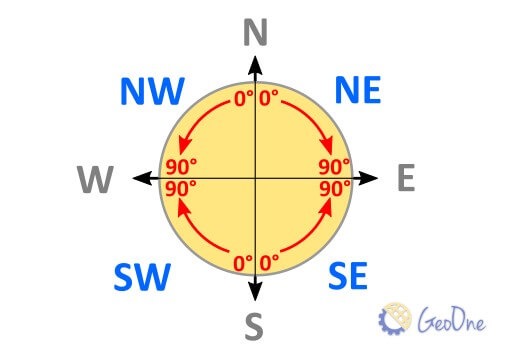
O Rumo é a direção de uma linha em relação aos pontos cardeais, medida a partir do Norte ou do Sul, com um ângulo menor ou igual a 90°. Ele é sempre acompanhado da indicação do quadrante (NE, SE, SW, NW).
Os rumos variam conforme o quadrante:
- NE (Nordeste): ângulos entre 0° e 90°.
- SE (Sudeste): ângulos entre 90° e 180°.
- SW ou SO (Sudoeste): ângulos entre 180° e 270°.
- NW ou NO (Noroeste): ângulos entre 270° e 360°.
Conversão de Azimutes para Rumos e Vice-Versa
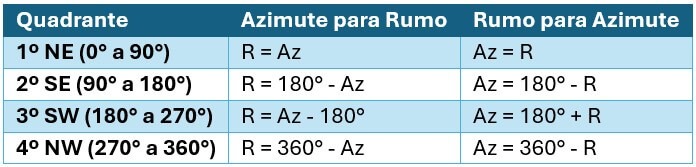
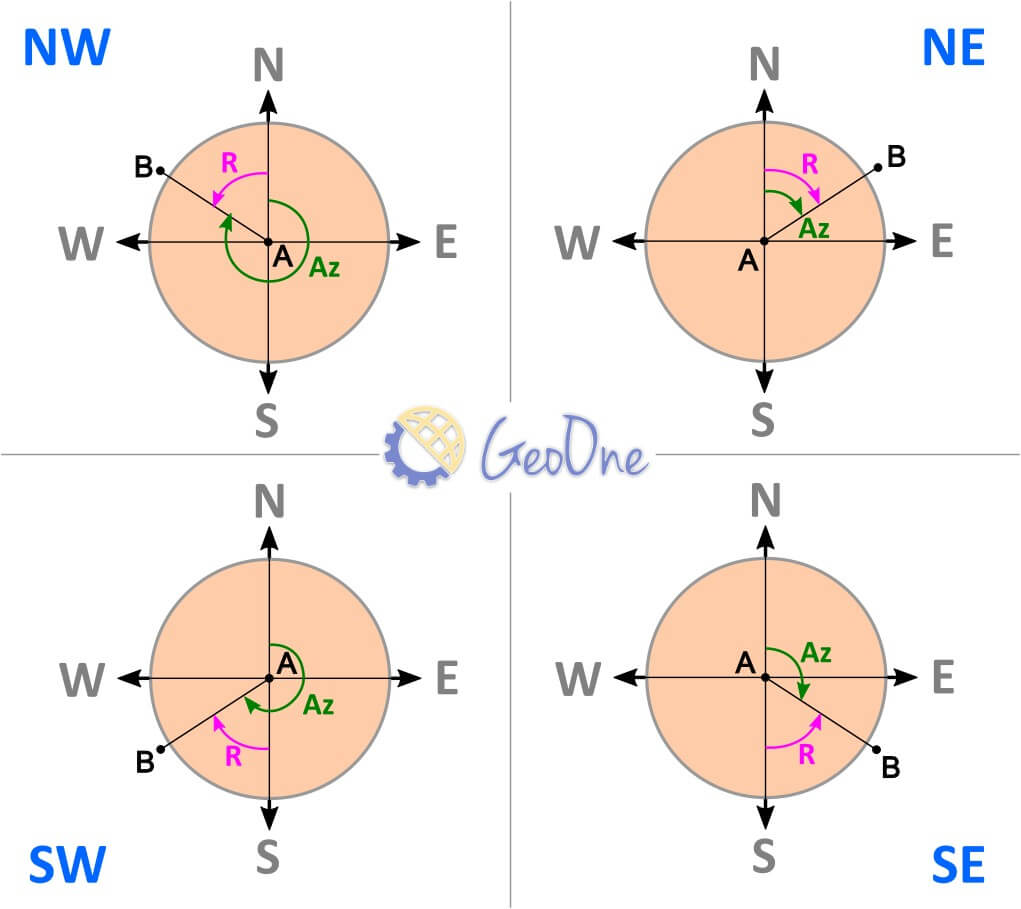
Para converter um azimute em rumo e vice-versa, é necessário identificar o quadrante em que a direção se encontra. O rumo é, então, o menor ângulo em relação ao eixo norte ou sul, acompanhado da indicação do quadrante.
A Tabela a seguir apresenta as fórmulas para o cálculo de Rumos e Azimutes de acordo com os diferentes quadrantes:
Ângulo Zenital
O ângulo zenital é a medida entre uma linha vertical que passa por um ponto e a linha de visada entre esse ponto e um objeto.
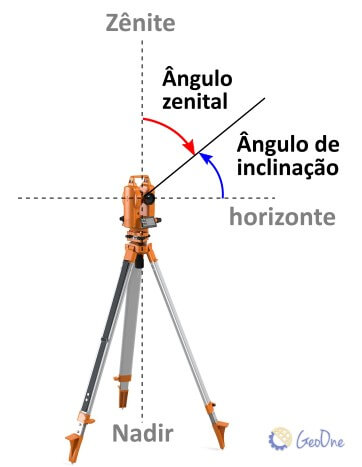
A relação entre o ângulo zenital e o ângulo inclinação é que ambos medem a distância angular entre uma linha de referência vertical e uma linha de visada. Essa relação decorre do fato de que o ângulo zenital é medido a partir da vertical (ou zênite), enquanto o ângulo de inclinação é medido em relação à horizontal. A soma do ângulo zenital e o ângulo de inclinação é igual a 90°.
Leituras Direta e Indireta
Na topografia, o ângulo horizontal e vertical é feito usando a média de leituras direta e indireta de um teodolito ou estação total. A média das duas medições minimiza possíveis erros sistemáticos, garantindo maior precisão.
Conversão entre GMS e Graus Decimais
A conversão entre graus, minutos e segundos (GMS) e graus decimais é uma operação comum na topografia, facilitando o cálculo de relações trigonométricas em algoritmos computacionais. A fórmula básica para essa conversão é:
(1) ![]()
Função Python para conversão de GMS para Graus decimais (extraído do plugin LFTools):
def dms2dd(txt):
newtxt =''
if (txt[-1]).upper() in ('W','O','S'):
if txt[0] != '-':
txt = '-' + txt[:-1]
else:
txt = txt[:-1]
elif (txt[-1]).upper() in ('E','L','N'):
txt = txt[:-1]
for letter in txt:
if not letter.isnumeric() and letter != '.' and letter != '-':
newtxt += '|'
else:
newtxt += letter
lista = newtxt[:-1].split('|')
if len(lista) != 3: # GMS
return None
else:
if '-' in lista[0]:
return -1*(abs(float(lista[0])) + float(lista[1])/60 + float(lista[2])/3600)
else:
return float(lista[0]) + float(lista[1])/60 + float(lista[2])/3600
Conversão de Graus Decimais para GMS
Para realizar a conversão inversa, transformamos a parte decimal do grau em minutos e, depois, a parte decimal dos minutos em segundos, facilitando a leitura em sistemas sexagesimais.
Função Python para conversão de Graus decimais para GMS (extraído do plugin LFTools):
def dd2dms(dd, n_digits):
if dd != 0:
graus = int(floor(abs(dd)))
resto = round(abs(dd) - graus, 10)
minutos = int(floor(60*resto))
resto = round(resto*60 - minutos, 10)
segundos = resto*60
if round(segundos,n_digits) == 60:
minutos += 1
segundos = 0
if minutos == 60:
graus += 1
minutos = 0
if dd < 0:
texto = '-' + str(graus) + '°'
else:
texto = str(graus) + '°'
texto = texto + '{:02d}'.format(minutos) + "'"
if n_digits < 1:
texto = texto + '{:02d}'.format(int(segundos)) + '"'
else:
texto = texto + ('{:0' + str(3+n_digits) + '.' + str(n_digits) + 'f}').format(segundos) + '"'
return texto
else:
return "0°00'" + ('{:0' + str(3+n_digits) + '.' + str(n_digits) + 'f}').format(0)
Algumas operações com ângulos no software QGIS
Transformação de Rumo em Azimute:
Conversão de GMS para graus decimais:
Ângulos internos e externos:
Aprenda a ganhar dinheiro com Topografia no QGIS
Conheça os cursos da GeoOne e domine o QGIS para Topografia!





















