Pesquisar
Close this search box.
Instagram Youtube

Categoria: ,

Produtos derivados de um MDE

Quais produtos podem ser gerados a partir de um MDE?

O Modelo Digital de Elevação (MDE) tem um papel fundamental em diversas análises, como por exemplo em estudos hidrológicos ou até mesmo resposta captada por imagens de satélites no sensoriamento remoto.
Neste post, vamos ver alguns produtos gerado a partir do MDE e seus conceitos, que são importantíssimos para servir de base na análise desses estudos que estão intrinsicamente relacionados a altimetria do relevo.

 

Declividade

 

A declividade ou inclinação é uma imagem (raster) em que os valores dos pixels correspondem ao ângulo que o plano tangente a uma superfície passando pelo centro do pixel faz com o plano do horizonte. Este ângulo é representado por α na Figura 1. Para o caso em que a declividade é medida em graus, seus valores podem variar de 0º a 90º.

Figura 1: Ângulo de Declividade

 

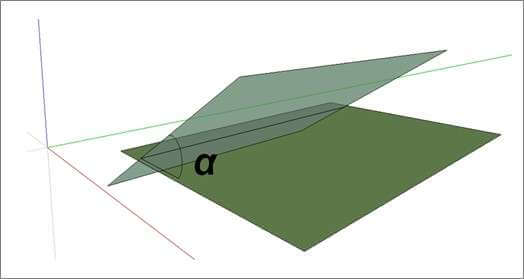
A declividade também pode ser interpretada pela percentagem ou grau máximo de mudança na elevação sobre a distância em cada ponto (SULLIVAN & UNWIN, 2010), sendo, neste caso, o cálculo da declividade dado através da Equação (1), onde Δh corresponde à variação de altitude para um valor distância horizontal  na direção de maior crescimento, ou seja, do gradiente da superfície.

 

(1)   \begin{equation*} Declividade_\%=\frac{\Delta h}{d}\times100\% \end{equation*}

Outra interpretação matemática leva em consideração que os valores de altitude z são função de x e y, ou seja,  z=f\left(x,y\right). Tendo em vista que a declividade é determinada pela taxa de variação de z em relação à superfície horizontal, ela é máxima na direção do gradiente da função  e, assim a taxa máxima de variação de z é dada por  (LEITHOLD, 1994), ou seja,

(2)   \begin{equation*} Declividade=\sqrt{\left(\left(\partial z/\partial x\right)^2+\left(\partial z/\partial y\right)^2\ \right)} \end{equation*}

Dentre os métodos para se determinar a declividade a partir de um MDE na forma matricial, os mais utilizados são os algoritmos da vizinhança e o da superfície quadrática (RODRÍGUEZ & SUÁREZ, 2010).

Os métodos citados usam uma máscara sobre o MDE para predizer a declividade no centro do pixel a partir dos seus oito vizinhos (Figura 2).

Figura 2: Máscara de Vizinhança

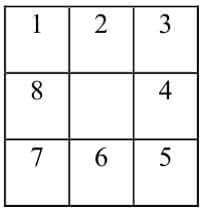
Pelo método da vizinhança (ESRI, 2011), as taxas de variação de z na direção x e y são calculadas utilizando as equações (3) e (4), respectivamente, onde d é o tamanho do pixel na mesma unidade de z.

(3)   \begin{equation*} \frac{\partial z}{\partial x}=\frac{\left(z_3+2\times z_4+z_5\right)-\left(z_1+2\times z_8+z_7\right)}{4\times2\times d} \end{equation*}

(4)   \begin{equation*} \frac{\partial z}{\partial y}=\frac{\left(z_1+2\times z_2+z_3\right)-\left(z_7+2\times z_6+z_5\right)}{4\times2\times d} \end{equation*}

Pelo método da superfície quadrática (ZEVENBERGEN & THORNE, 1987), as taxas de variação de z na direção x e y são determinadas por meio das equações (5) e (6), respectivamente:

(5)   \begin{equation*} \frac{\partial z}{\partial x}=\frac{z_4-z_8}{2\times d} \end{equation*}

(6)   \begin{equation*} \frac{\partial z}{\partial y}=\frac{z_2-z_6}{2\times d} \end{equation*}

A declividade para ambos os métodos pode ser calculada em graus pela equação (7) aplicando-se a função arco-tangente na equação (2), ou seja,

(7)   \begin{equation*} Declividade_\angmsd=tg^{-1}\left(\sqrt{\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}\right) \end{equation*}

 

 

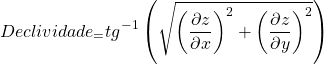
Aspecto

 

O aspecto corresponde ao ângulo medido no sentido horário que o vetor gradiente faz com a direção norte ou eixo y (SULLIVAN & UNWIN, 2010).

A imagem do aspecto complementa a imagem de declividade, pois dá o azimute para a direção de maior ascensão em um determinado ponto no terreno.

A Figura 3 apresenta a imagem do aspecto (lado direito) calculada a partir do MDE da região do lado esquerdo. Cada cor indica uma direção do vetor gradiente, sendo uma associação entre a matiz de cores com as direções de 0º a 360º.

Figura 3 : (a) Imagem do terreno (b) Imagem do Aspecto

 

 

Relevo Sombreado (Hillshade)

 

O relevo sombreado é uma técnica de visualização da superfície do terreno onde se busca retratá-lo da maneira como ele se apresentaria em variações de brilho, considerando uma fonte virtual e oblíqua de iluminação. Seus resultados são gradientes de brilho que dão a aparência de uma superfície tridimensional em um mapa (ALBERTZ & WIGGENHAGEN, 2009).

O gradiente de brilho é proporcional a cosθ (aplicação da Lei de Lambert para radiação), onde θ corresponde ao ângulo entre o vetor normal à superfície e o vetor incidente de iluminação vinda da fonte pontual (ALBERTZ & WIGGENHAGEN, 2009), tal situação é ilustrada na Figura 4.

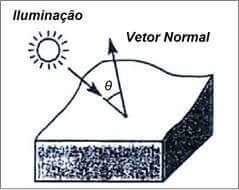
Figura 4: Ângulo entre o vetor de iluminação e o vetor normal a superfície
(Adaptado de ALBERTZ & WIGGENHAGEN, 2009)

A fonte virtual, na grande parte das vezes, busca simular o sol cuja posição é determinada pelo ângulo zenital e azimute solar. Esses parâmetros podem ser calculados se conhecidas a época do ano, o horário de aquisição da cena e a posição geográfica.

O valor do ângulo zenital θ solar pode ser calculado com a equação (8), onde φ é o valor da latitude e δ a declinação do sol para o dia do ano D. O valor de H corresponde ao ângulo horário que depende da longitude λ e da hora do dia em UTC (SOBRINHO et al, 2007).

(8)   \begin{equation*} \cos{\theta}=sen\varphi.sen\delta+\cos{\varphi}.\cos{\delta}.\cos{H} \end{equation*}

(9)   \begin{equation*} \delta=23,45^{\circ}.sen\left(\frac{360^{\circ}.D}{365}-80^{\circ}\right) \end{equation*}

(10)   \begin{equation*} t_{UTC}=t_{local}+FUSO \end{equation*}

(11)   \begin{equation*} h=mod{\left(\ t_{UTC}+\frac{\lambda}{15,24}\right)} \end{equation*}

(12)   \begin{equation*} H=\left(h-12\right)\times15º \end{equation*}

O azimute solar Az, calculado pela equação (13), pode ser dado em graus e corresponde ao ângulo que a projeção do sol no plano do horizonte faz com o norte.

(13)   \begin{equation*} \cos{A}z=\frac{sen\delta-\cos{\theta}.s{e}n\varphi}{sen\theta.\cos{\varphi}} \end{equation*}

Munido dos ângulos zenital θ e azimute solar Az, além das imagens de declividade d e aspecto a é possível determinar o índice de relevo sombreado RS pela equação (14), (ESRI, 2011):

(14)   \begin{equation*} RS=255\times\left[\cos{\theta}.\cos{d}-sen\theta.send.\cos{\left(\ Az-a\right)}\right] \end{equation*}

 

Curvas de Nível (Isolinhas ou Contornos)

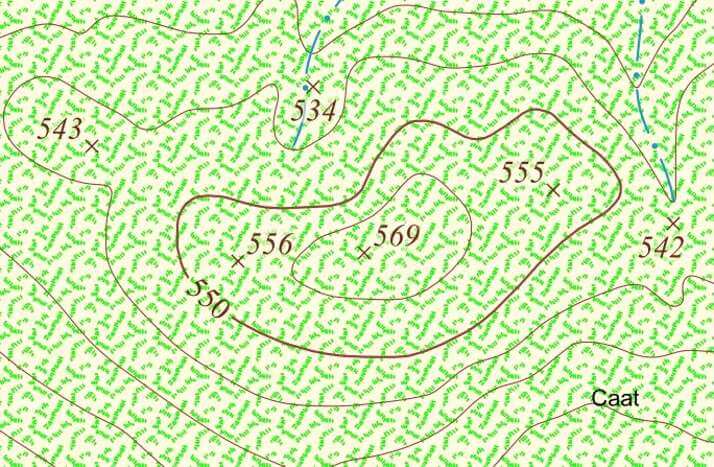
Curvas de nível é uma série de pontos conectados com mesma cota (elevação), sendo mais utilizadas para ilustrar o relevo no mapa.
Para a altimetria, as curvas de nível devem mostrar as altitudes acima do nível do mar (Mean Sea Level – MSL).
Os intervalos das curvas de nível são chamadas de equidistâncias e podem ser classificadas em:

  • Curvas mestras – curva mais destacada e de maior equidistância, costuma ser rotulada.
  • Curvas normais – curva de espessura mais fina e de menor equidistância (mais próximas), costuma não ser rotulada.
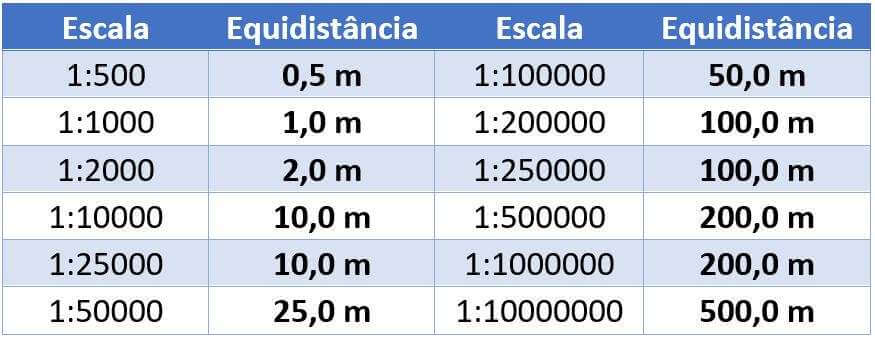
Figura 5: Exemplo de curvas mestra e simples.

A equidistância entre as curvas depende da escala e do propósito do mapa, pois linhas muito próximas ou demasiadamente afastadas dificultam a leitura do mapa. Mas, em geral, os valores da Tabela a seguir atendem a maioria dos casos para diversas escalas do mapeamento sistemático:

Figura 6: Equidistâncias entre curvas de nível.

A geração de curvas de nível é feita a partir do Modelo Digital do Terreno (MDT), mas antes deve ser realizado um tratamento para remover ruídos através de um filtro da mediana e, posteriormente, deve ser aplicada uma suavização.  Para que o seu trabalho fique perfeito, um tratamento no resultado vetorial deve também ser feito, eliminando-se linhas pequenas, além de um processo de generalização e suavização, até que o resultado fique satisfatório. Aprenda todos esses passos em nossa metodologia completa de geração de curvas de nível no curso de Processamento de Imagens de Drone no WebODM e QGIS.

 

Gerando produtos a partir do MDE no QGIS

Deseja aprender mais como utilizar um MDE para o cálculo de Declividade, Aspecto e Relevo Sombreado na elaboração de mapas hipsométricos incríveis? Então assista nossa aula no YouTube:

Quer aprender mais sobre QGIS?

CLIQUE AQUI PARA SE INSCREVER NA ÁREA DE MEMBROS DA GEOONE

JÁ SOU UM GEONISTA!

 

CLIQUE AQUI PARA SABER A DIFERENÇA ENTRE MDT E MDS!

Referências:

ALBERTZ, J; WIGGENHAGEN, M. Guide for Photogrammetry and Remote Sensing. 5th completely revised and extended edition. Wichmann. 2009.

ESRI. ArcGIS Resource Center: How Hillshade works. 2011. Disponível em: < http://help.arcgis.com/en/arcgisdesktop/10.0/help/index.html#//009z000000z2000000.htm>. Acesso em: 03/06/2015.

FRANÇA, L. Mapa da Evolução Espaço-temporal da Cobertura Vegetal no Município do Rio de Janeiro de 1985 a 2015. Projeto de Fim de Curso. Instituto Militar de Engenharia. Rio de Janeiro. 2015.

FRANÇA, L. L. S.; SILVA, L. F. C. F.; SILVA, W. B. Mapping of the spatial-temporal change for vegetation canopy in rough relief areas. R. bras. Geom., Curitiba, v. 5, n. 3, p. 343-360, jul/set. 2017. Available from: https://www.researchgate.net/publication/320020755_Mapping_of_the_spatial-temporal_change_for_vegetation_canopy_in_rough_relief_areas

LEITHOLD, Louis. O Cálculo com Geometria Analítica. Parte 2. 3ª edição. pg. 976. Editora HARBRA. 1994.

RODRÍGUEZ, J.; SUARÉZ M. Comparison of Mathematical Algorithms for Determining the Slope Angle in GIS Environment. Aqua – LAC, vol. 2, nº 2, pg. 78-82. 2010.

SOBRINHO, J. et al. Determinação de ângulos das relações Terra-Sol para fins de orientação de pomares e poda de árvores em Mossoró-RN. 2007.

SULLIVAN, David O.; UNWIN, David J. Geographic Information Analysis. 2nd edition. Wiley and Sons. 2010.

ZEVENBERGEN, L.; THORNE, C. Quantitative Analysis of Land Surface Topography: Earth Surface Processes and Landforms, vol. 12, pg. 47-56. 1987.

 

Compartilhes nas redes Sociais

ÚLTIMOS POSTS
CONHEÇA NOSSOS CURSOS
Curso drone
Python para QGIS
Sensoriamento Remoto com QGIS
Leandro França

Politica de Privacidade

FALE CONOSCO
contato@geoone.com.br

Instagram Youtube