Como calcular o Azimute de Puissant?
Segundo o Manual Técnico de Georreferenciamento do INCRA (2022), o cálculo de azimute deve ser realizado conforme o formulário do Problema Geodésico Inverso segundo Puissant, sendo expresso no sistema sexagesimal. Embora o Manual forneça essa orientação, ele não apresenta as fórmulas específicas para o cálculo desse azimute. Para suprir essa lacuna e contribuir com a comunidade da GeoOne, além de apresentar as fórmulas, disponibilizamos também um algoritmo Python para o cálculo do Azimute de Puissant.
Ao fim do artigo, fazemos uma breve comparação entre o Azimute de Puissant e outros tipos de azimute, como o Azimute Plano, calculados na projeção UTM, Azimute Verdadeiro (com correção da convergência meridiana), e o Azimute no plano do Sistema Geodésico Local (SGL), todos obtidos no QGIS com o plugin LFTools.
Sobre Puissant
Louis Puissant, nascido em 1769 na França, foi um destacado geodesista e matemático que fez importantes contribuições para a topografia. Ele serviu como oficial no corpo de engenheiros topográficos do exército francês e foi professor na École Centrale d’Agen. Em 1805, publicou sua obra mais famosa, “Traité de Géodésie”, que se tornou uma referência na área da geodésia. Suas fórmulas geodésicas, desenvolvidas para cálculos de azimute e distâncias, foram amplamente adotadas devido à sua precisão e simplicidade, facilitando a medição e representação da superfície terrestre.
Evolução dos métodos de cálculo de Azimute Geodésico
A adaptação moderna das fórmulas de Puissant continua a ser utilizada devido à sua precisão e facilidade de uso, especialmente em levantamentos de média distância. Comparado com outros métodos, como as fórmulas de Bessel e Vincenty, as fórmulas de Puissant são menos complexas e ainda mantêm alta precisão para distâncias moderadas. Embora os métodos de Vincenty sejam mais precisos para longas distâncias, utilizando técnicas iterativas, as fórmulas de Puissant são preferidas em aplicações onde a simplicidade e a rapidez são críticas, sem sacrificar significativamente a exatidão.
As fórmulas de Puissant são recomendadas para distâncias de até 80 km. Elas são conhecidas por sua precisão de até 1 parte por milhão (1 mm por 1 km), tornando-as adequadas para levantamentos topográficos de média distância. Embora existam métodos mais precisos para longas distâncias, como as fórmulas de Vincenty, as fórmulas de Puissant continuam a ser valorizadas por sua simplicidade e eficiência em aplicações práticas onde a rapidez e a facilidade de uso são essenciais.
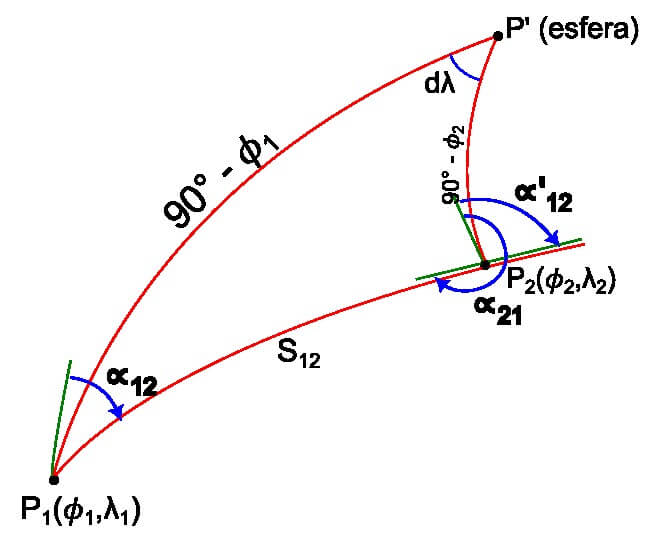
Fórmulas para o cálculo de Azimute de Puissant para o Problema Geodésico Inverso
Segundo o MT GIR (INCRA, 2022), o cálculo de azimute deve ser realizado conforme o formulário do Problema Geodésico Inverso segundo Puissant e o valor deve ser expresso no sistema sexagesimal. Abaixo seguem as fórmulas que devem ser empregadas, onde é calculado o azimute de P1(ϕ1, λ1) para P2(ϕ2, λ2) , sendo a e f o semieixo maior e achatamento elipsoide, respecitvamente.
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
(15) ![]()
(16) ![]()
(17) ![]()
Obs.: Fórmulas disponibilizadas pelo Departamento de Cartografia de UFPR.
Algoritmo Python para determinar o Azimute de Puissant
Para facilitar ainda mais o desenvolvimento de aplicações, disponibilizamos também o algoritmo Python da função que calcula o azimute de Puissant dentro do plugin LFTools:
from math import cos, sin, radians, degrees, atan2
import numpy as np
def AzimutePuissant(lat1, lon1, lat2, lon2, a = 6378137, f = 1/298.257222101):
"""
Calcula o azimute segundo Puissant entre dois pontos geodésicos.
Parâmetros:
lat1, lon1: Latitude e longitude do ponto inicial em graus.
lat2, lon2: Latitude e longitude do ponto final em graus.
a: Semi-eixo maior do elipsoide (padrão: 6378137 metros).
f: Achatamento do elipsoide (padrão: 1/298.257222101).
Retorna:
Azimute em graus.
"""
e2 = 2*f - f**2 # Calcula a excentricidade quadrada (e^2) a partir do achatamento (f)
seno_1segundo = sin(radians(1/3600))
lat_media = (radians(lat1) + radians(lat2)) / 2
seno_lat_media = sin(lat_media)
cos_lat_media = cos(lat_media)
pow_seno_20 = pow(seno_lat_media, 2)
Nm = a / (pow(1 - (e2 * pow_seno_20), 0.5))
delta_lat = (lat2 - lat1) * 3600
delta_lon = (lon2 - lon1) * 3600
Mm = (a * (1 - e2)) / pow(1 - (e2 * pow_seno_20), 1.5)
Bm = 1 / (Mm * seno_1segundo)
x = delta_lon * cos_lat_media * Nm * seno_1segundo
y = delta_lat * cos(radians(delta_lon / 7200))/Bm
F = (1 / 12) * seno_lat_media * cos_lat_media * cos_lat_media * seno_1segundo * seno_1segundo
gamma = (delta_lon * seno_lat_media * (1 / cos(radians(delta_lat / 7200))) + (F * delta_lon * delta_lon * delta_lon))
Azimute = degrees(math.atan2(x, y)) - (gamma / 7200)
return (Azimute + 360)%360
# Exemplo de uso:
lat1, lon1 = -23.5505, -46.6333 # São Paulo, Brasil
lat2, lon2 = -22.9083, -43.1964 # Rio de Janeiro, Brasil
Azimute = AzimutePuissant(lat1, lon1, lat2, lon2)
print(f"Azimute de P1 para P2: {Azimute:.3f} graus")
Curso de Python da GeoOne
Se você ainda não domina Python para a Topografia, convido a conhecer nosso curso que vai lhe permitir dominar essa linguagem para a sua área de atuação:
Comparação dos resultados de Azimutes obtidos no plugin LFTools
Para comparação dos resultados, foi adotado um imóvel aleatório consultado com a ferramenta “Consulta a base do INCRA” do plugin GeoINCRA.
Definições:
- Azimute Plano: Azimute calculado no plano de projeção UTM ou outra projeção cartográfica.
- Azimute Verdadeiro: Azimute Plano com a correção da convergência meridiana.
- Azimute de Puissant: Azimute calculado com as fórmulas de Puissant para o Problema Inverso da Geodésia.
- Azimute no SGL: Azimute no plano do Sistema Geodésico Local (SGL).
Tabela 1: Comparação entre diferentes tipos de azimutes calculados no QGIS com o plugin LFTools.
| VÉRTICE | COORDENADA | AZIMUTE | DISTÂNCIA | |||||
| E | N | PLANO | VERDADEIRO | SGL | PUISSANT | UTM (m) | SGL (m) | |
| DQA-M-2204 | 273.921,83 | 9.209.463,84 | 181°40’48,2″ | 181°56’05,5″ | 181°56’13,9″ | 181°56’05,6″ | 203,97 | 203,92 |
| DQA-M-2394 | 273.915,85 | 9.209.259,96 | 181°40’44,6″ | 181°56’02,1″ | 181°56’10,7″ | 181°56’02,4″ | 403,40 | 403,31 |
| DQA-P-13684 | 273.904,03 | 9.208.856,73 | 217°51’49,9″ | 218°07’07,9″ | 218°09’15,7″ | 218°07’09,3″ | 3.009,89 | 3.009,20 |
| DQA-M-2389 | 272.056,60 | 9.206.480,51 | 339°49’26,3″ | 340°04’54,7″ | 340°03’33,1″ | 340°04’54,1″ | 1.080,35 | 1.080,10 |
| DQA-M-3720 | 271.683,98 | 9.207.494,57 | 319°52’51,2″ | 320°08’19,9″ | 320°06’17,0″ | 320°08’19,5″ | 944,93 | 944,71 |
| GMJR-M-0088 | 271.075,08 | 9.208.217,17 | 62°54’30,6″ | 63°10’00,9″ | 63°11’36,8″ | 63°10’00,4″ | 1.934,69 | 1.934,23 |
| DQA-M-3722 | 272.797,50 | 9.209.098,25 | 71°59’14,7″ | 72°14’37,0″ | 72°15’45,8″ | 72°14’36,8″ | 1.182,27 | 1.182,00 |
Como gerar o memorial descritivo com azimute de Puissant no LFTools
Veja como é fácil e prático gerar o memorial descritivo com azimutes de Puissant no QGIS com o plugin LFTools:
Assista também:
Comparação com os Azimutes de um Memorial do SIGEF
A Tabela 2, apresenta os resultados de azimutes de Puissant obtidos com o plugin LFTools em comparação aos gerados no SIGEF. Observa-se que ambos são praticamente iguais. No entanto, os resultados do plugin LFTools são mais precisos, pois são expressos em décimos de segundos, enquanto no SIGEF os valores são arredondados aos minutos, não seguindo completamente o sistema sexagesimal, conforme orientado no próprio MT GIR do INCRA.
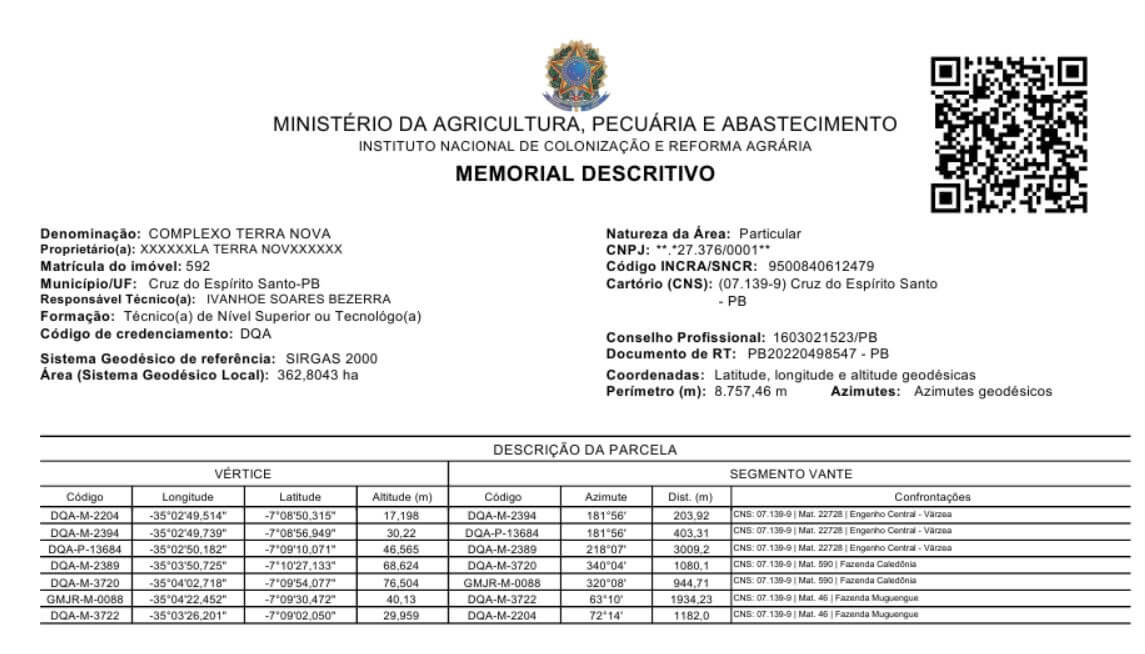
Tabela 2: Comparação entre os azimutes e distâncias calculados no LFTools e gerados no SIGEF.
| VÉRTICE | AZIMUTE | DISTÂNCIA | ||
| SIGEF | LFTools | SIGEF | LFTools | |
| DQA-M-2204 | 181°56′ | 181°56’05,6″ | 203,92 | 203,92 |
| DQA-M-2394 | 181°56′ | 181°56’02,4″ | 403,31 | 403,31 |
| DQA-P-13684 | 218°07′ | 218°07’09,3″ | 3009,2 | 3.009,20 |
| DQA-M-2389 | 340°04′ | 340°04’54,1″ | 1080,1 | 1.080,10 |
| DQA-M-3720 | 320°08′ | 320°08’19,5″ | 944,71 | 944,71 |
| GMJR-M-0088 | 63°10′ | 63°10’00,4″ | 1934,23 | 1.934,23 |
| DQA-M-3722 | 72°14′ | 72°14’36,8″ | 1182,0 | 1.182,00 |
Apesar dessa pequeníssima diferença, atualmente, a prática comum não é usar azimutes e distâncias para reconstituir um memorial descritivo, mas sim utilizar coordenadas geodésicas ou as coordenadas projetadas (UTM). Essas coordenadas necessitam ter a precisão necessária para garantir a acurácia posicional do imóvel georreferenciado.
Onde Dominar o QGIS para a Topografia: Combo GeoOne
A GeoOne oferece cursos abrangentes, como o Curso de Automatização no QGIS para Gerar Plantas e Memoriais com apenas 3 cliques e o Curso de Georreferenciamento de Imóveis Rurais para gerar a planilha ODS do SIGEF/INCRA no QGIS. Além disso, há muitos outros cursos disponíveis, incluindo Python, OpenDroneMap, RTKLib, QField, Inkscape, CloudCompare e muito mais. Adquirir o pacote com todos os cursos da GeoOne é a melhor forma de se tornar um especialista completo em topografia e geoprocessamento.






















