Pesquisar
Close this search box.
Instagram Youtube

Categoria:

Sistema Geodésico Local (SGL)

Como calcular área no SGL?

Realizar o cálculo exato de área de um imóvel de grande extensão sempre foi um desafio. Vários fatores podem interferir nos resultados, por exemplo, a técnica de levantamento topográfico, a precisão dos equipamentos, o tipo de projeção e suas distorções, além da altitude média onde esse imóvel se localiza. Esses fatores, muitas vezes, passam despercebidos por profissionais de agrimensura e geoprocessamento.

A norma do INCRA estabelece em seu Manual Técnico de Posicionamento que a área de imóveis rurais deve ser calculada a partir de coordenadas referenciadas ao Sistema Geodésico Local (SGL), tal procedimento possibilita resultados praticamente em “verdadeira grandeza” quando comparado aos valores reais medidos no Terreno, obtendo-se áreas e perímetros mais fieis, se comparado às projeções cartográficas mais comuns.

Neste post, vamos explicar alguns conceitos e explorar referências relacionadas ao SGL, apresentando suas fórmulas matemáticas e mostrando como esses cálculos podem ser executados na prática com Python ou no próprio plugin LFTools, utilizando o software QGIS.

 

O que é um Sistema Geodésico Local (SGL)?

O SGL consiste em um sistema de referência de coordenadas de eixos ortogonais (E, N, U), onde o eixo “N” aponta para o norte geodésico, o eixo “E” aponta para a direção leste, estando ambos contidos no plano perpendicular a normal ao elipsoide que passa por um ponto arbitrado como origem do sistema, com o eixo “U” coincidindo com a direção desta normal (Figura 1).

Figura 1: Sistema Geodésico Local (SGL).

Agora vamos entender melhor os sistemas de coordenas apresentados na Figura 1, detalhando o que vem a ser coordenadas geodésicas, geocêntricas e topocêntricas.

Coordenadas geodésicas (λ, ϕ, h)

Coordenadas geodésicas remete a um sistema de coordenadas baseado em um elipsoide, com coordenas as curvilíneas: latitude geodésica ϕ (na direção norte/sul) e longitude geodésica λ na (na direção leste/oeste); e a altitude geodésica h (também conhecida como altitude elipsoidal ou geométrica).

 

Coordenadas geocêntricas (X, Y, Z)

O sistema de coordenadas geocêntricas, também conhecidas como ECEF, do Earth-centered, Earth-fixed, é um sistema de referência espacial cartesiano que representa qualquer local nas proximidades da Terra, incluindo sua superfície, interior, atmosfera e áreas externas circundantes no espaço, sendo mais utilizada para o rastreio de órbitas de satélites no posicionamento GNSS.

Suas medidas X, Y e Z tem como origem o centro de massa da Terra, coincidindo aproximadamente o eixo Z com o seu eixo de rotação, e o eixo X (positivo) direcionado ao ponto de encontro da linha do Equador com o Meridiano de Greenwich.

 

Coordenadas topocêntricas (E, N, U)

As coordenadas ENU são formadas considerando-se um plano perpendicular à normal ao elipsoide passando por um ponto de origem, fixado em um local específico.

As medidas lineares são dadas em metros para os seguintes eixos:

  • East (E), na direção da linha do paralelo de origem;
  • North (N), na direção da linha meridiana de origem; e
  • Up (U), na direção da normal ao elipsoide.

 

Como definir um Sistema Geodésico Local?

Para a transformação de coordenadas geodésicas ou geocêntricas em coordenadas topocêntricas no SGL, primeiro é necessário definir o elipsoide, ou seja, os parâmetros de semi-eixo maior e achatamento. Por exemplo, no caso de utilização do Sistema Geodésico de Referência SIRGAS2000, o elipsoide GRS80 tem a = 6.378.137m (semi-eixo maior) e f = 298.257222101 (achatamento).

O segundo critério deve ser adotar um ponto de origem para o sistema, de preferência sendo o ponto centroide do polígono da área mapeada, considerando-se a média das altitudes na região (França et al, 2020).

De acordo com o INCRA, deve-se adotar a média das coordenadas da parcela em questão como origem do sistema, para a conversão de coordenadas cartesianas geocêntricas para o SGL (INCRA, 2013a).

É importante ressaltar que a NBR 14.166 de 1998 alerta sobre a área máxima de abrangência do sistema que considera o plano tangente ao elipsoide de referência. Como ocorre uma abstração da curvatura da terra nessa extensão, os valores de 50 Km x 50 Km não devem ser ultrapassados (ABNT, 1998), pois fora desses limites os erros são bastante acentuados.

 

Qual a principal diferença de um Sistema Geodésico Local e Topográfico Local?

O Sistema Geodésico Local (SGL) é adotado nos trabalhos de georreferenciamento de imóveis rurais e, segundo o Manual Técnico de Posicionamento (INCRA, 2013a), pode ser aplicado no cálculo de áreas, no uso do método de posicionamento por geometria analítica e em projetos de parcelamento/desmembramento (Simões et al, 2017).

Já o Sistema Topográfico Local (STL), segundo a NBR 14166/98, consiste no sistema de representação, em planta, das posições relativas de pontos de um levantamento topográfico com origem em um ponto de coordenadas geodésicas conhecidas (ABNT, 1998). No Brasil, o STL é adotado em levantamentos por alguns municipais para fins de cadastro.

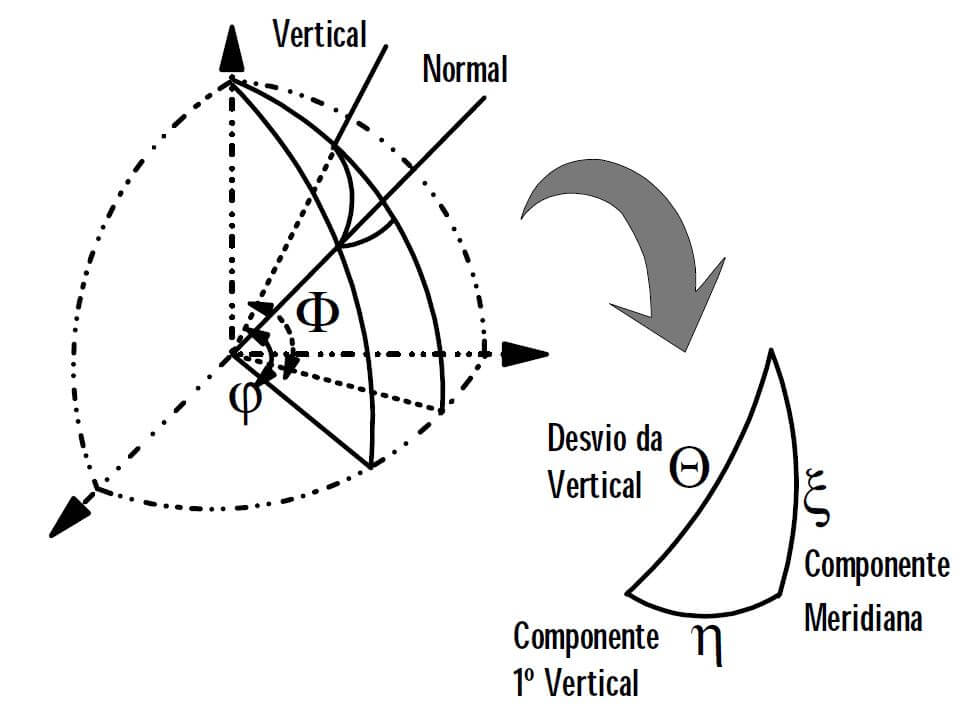
Resumidamente, no SGL o plano é perpendicular à Normal ao elipsoide, já no STL o plano é perpendicular à Vertical (linha de prumo), e coincide com o horizonte da estação. Já a direção dos eixo norte-sul é dada pelo meridiano astronômico do lugar. O SGL é mais adequado para trabalhar com dados GNSS, já o STL é mais indicado para trabalhos com Estação Total, Teodolitos e Níveis, pois é possível calcular os componentes do desvio da vertical e transformação do STL para o SGL.

Figura 2: Comparação entre SGL e STL. Fonte: Notas de aula de Geodésia, IME.

 

Como realizar a transformação de coordenadas geodésicas para o SGL?

 

Para a transformação entre os sistemas de coordenadas geodésicas, geocêntricas e topocêntricas, podem ser utilizas as equações e algoritmos apresentados a seguir.

Geodésicas para geocêntricas

Fórmulas:

(1)   \begin{equation*} e^2=f(2-f) \end{equation*}

(2)   \begin{equation*} N=a/\sqrt{1-e^2\cdot{sen}^2{\left(\varphi\right)}} \end{equation*}

(3)   \begin{equation*} X=\left(N+h\right)\cdot c o s{\left(\varphi\right)}\cdot c o s{\left(\lambda\right)} \end{equation*}

(4)   \begin{equation*} Y=\left(N+h\right)\cdot\ c\ o\ s{\left(\varphi\right)}\cdot\ s\ e\ n{\left(\lambda\right)} \end{equation*}

(5)   \begin{equation*} Z=\left(N(1-e^2)+h\right)\cdot s i n{\left(\varphi\right)} \end{equation*}

Algoritmo (Python):

# Conversão de coordenadas geodésicas para geocêntricas
def geod2geoc(lon, lat, h, a, f):
    lon = radians(lon)
    lat = radians(lat)
    e2 = f*(2-f) # primeira excentricidade
    N = a/sqrt(1-(e2*sin(lat)**2))
    X = (N+h)*cos(lat)*cos(lon)
    Y = (N+h)*cos(lat)*sin(lon)
    Z = (N*(1-e2)+h)*sin(lat)
    return (X,Y,Z)

 

Geocêntricas para geodésicas

(conforme Resoluções do IGBE, 1989 e 2005)

Fórmulas:

(6)   \begin{equation*} b=a\left(1-f\right) \end{equation*}

(7)   \begin{equation*} e_2^2=e^2/\left(1-e^2\right) \end{equation*}

(8)   \begin{equation*} tg{\left(u\right)}=\left(\frac{a}{b}\right)\cdot Z/\sqrt{X^2+Y^2} \end{equation*}

(9)   \begin{equation*} sen{\left(u\right)}=\frac{tg{\left(u\right)}}{\sqrt{{tg}^2{\left(u\right)}+1}} \end{equation*}

(10)   \begin{equation*} cos{\left(u\right)}=\frac{1}{\sqrt{{tg}^2{\left(u\right)}+1}} \end{equation*}

(11)   \begin{equation*} \lambda=arctg{\left(\frac{Y}{X}\right)} \end{equation*}

(12)   \begin{equation*} \varphi=\tg^{-1}{\left(\frac{Z+e_2^2\cdot b\cdot sen^3\left(u\right)}{\sqrt{X^2+Y^2}-e^2.a.cos^3\left(u\right)}\right)} \end{equation*}

(13)   \begin{equation*} h=\sqrt{X^2+Y^2}/cos{\left(\varphi\right)}-N \end{equation*}

Algoritmo (Python):

# Conversão de coordenadas geocêntricas para geodésicas
def geoc2geod(X, Y, Z, a, f):
    b = a*(1-f)
    e2 = f*(2-f) # primeira excentricidade
    e2_2 = e2/(1-e2) # segunda excentricidade
    tg_u = (a/b)*Z/sqrt(X**2 + Y**2)
    sen_u = tg_u/sqrt(1+tg_u**2)
    cos_u = 1/sqrt(1+tg_u**2)
    lon =arctan(Y/X)
    lat = arctan( (Z+ e2_2 * b * sen_u**3) / (sqrt(X**2 + Y**2) - e2 * a * cos_u**3))
    N = a/sqrt(1-(e2*sin(lat)**2))
    h = sqrt(X**2 + Y**2)/cos(lat) - N
    lon = lon/pi*180
    lat = lat/pi*180
    return (lon, lat, h)

 

Geocêntricas para Topocêntricas

Fórmula:

(14)   \begin{gather*} \begin{bmatrix} E \\ N\\U \end{bmatrix} = \begin{bmatrix} -sen(\lambda)&cos\funcapply(\lambda)&0\\ -sen(\varphi).co\ s\funcapply(\lambda)&-sen(\varphi).sen(\lambda)&co\ s\funcapply(\varphi)\\ cos\funcapply(\varphi).co\ s\funcapply(\lambda)&\cos\funcapply(\varphi).sen(\lambda)&sen(\varphi) \end{bmatrix} . \begin{bmatrix} X-X_{0} \\ Y-Y_{0}\\Z-Z_{0} \end{bmatrix} + \begin{bmatrix}150.000 \\ 250.000\\0 \end{bmatrix} \end{gather*}

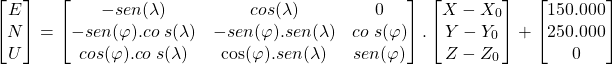
Algoritmo (Python):

# Conversão de Coordenadas Geocêntrica para Topocêntricas
def geoc2enu(X, Y, Z, lon0, lat0, Xo, Yo, Zo):
    lon = radians(lon0)
    lat = radians(lat0)

    M = matrix(
    [
    [  -sin(lon),                     cos(lon),                 0 ],
    [  -sin(lat)*cos(lon),   -sin(lat)*sin(lon),          cos(lat)],
    [   cos(lat)*cos(lon),    cos(lat)*sin(lon),          sin(lat)]
    ]
    )

    T = matrix(
    [[X - Xo], [Y-Yo], [Z-Zo]]
    )

    Fo = matrix([[15e4],[25e4],[0]]) # False E and N

    R = M*T + Fo
    return (R[0,0], R[1,0], R[2,0])

 

 

Topocêntricas para Geocêntricas

Fórmula:

(15)   \begin{gather*} \begin{bmatrix} X \\ Y\\Z \end{bmatrix} = \left[\begin{matrix}-sen\left(\lambda\right)&-sen\left(\varphi\right).cos{\left(\lambda\right)}&\cos{\left(\varphi\right)}.cos{\left(\lambda\right)}\\cos{\left(\lambda\right)}&-sen\left(\varphi\right).sen\left(\lambda\right)&\cos{\left(\varphi\right)}.sen\left(\lambda\right)\\0&\cos{\left(\varphi\right)}&sen\left(\varphi\right)\\\end{matrix}\right] . \begin{bmatrix} E-150.000 \\ N-250.000\\U \end{bmatrix} + \begin{bmatrix} X_{0} \\ Y_{0}\\Z_{0} \end{bmatrix} \end{gather*}

Algoritmo (Python):

# Conversão de Coordenadas Topocêntricas para Geocêntrica
def enu2geoc(E, N, U, lon0, lat0, Xo, Yo, Zo):
    lon = radians(lon0)
    lat = radians(lat0)

    Fo = matrix([[15e4],[25e4],[0]]) # False E and N

    M = matrix(
    [
    [  -sin(lon),     -sin(lat)*cos(lon),          cos(lat)*cos(lon)],
    [  cos(lon),      -sin(lat)*sin(lon),          cos(lat)*sin(lon)],
    [   0        ,              cos(lat),                       sin(lat)     ]
    ]
    )

    T = matrix(
    [[E], [N], [U]]
    )

    R = M*(T-Fo) + [[Xo], [Yo], [Zo]]
    return (R[0,0], R[1,0], R[2,0])

 

 

Como calcular a área no SGL?

Para o cálculo de área no SGL é necessário que o polígono tenha coordenadas com a dimensão Z.

O QGIS segue os padrões da Open Geospatial Consortium (OGC) e esse tipo de geometria é definido como PolygonZ, ou MultiPolygonZ, para uma coleção de geometrias do tipo polígono.

Para o cálculo de área no SGL, é possível utilizar as formulações e algoritmos disponibilizados acima para transformação de coordenadas, ou simplesmente utilizar as ferramentas e funções do plugin LFTools diretamente no QGIS.

Assista a aula abaixo e confira como é simples e prático fazer essas transformações:

Se você deseja aprender mais sobre o uso do QGIS para realizar trabalhos profissionais de forma automatizada, então lhe convidamos a conhecer nosso curso de Automatização de Plantas e Memoriais Descritivos no QGIS com apenas 3 cliques:

CLIQUE AQUI

 

Inscreva-se em nossa plataforma de cursos:

QUERO ME TORNAR UM GEONISTA

YouTube

Instagram

 

REFERÊNCIAS

 

ABNT. NBR 14166: 1998. Rede de Referência Cadastral Municipal – Procedimento.

IBGE. (1989). Resolução No 23, de 21 de fevereiro de 1989.

IBGE. (2005). Resolução No 01, de 25 de fevereiro de 2005.

INCRA. MANUAL TÉCNICO DE POSICIONAMENTO: Georreferenciamento de Imóveis Rurais. 1ª Edição. Brasília. 2013a. Disponível em: manual_tecnico_posicionamento_1ed.pdf (incra.gov.br)

INCRA. NORMA TÉCNICA PARA GEORREFERENCIAMENTO DE IMÓVEIS RURAIS. 3ª Edição. Brasília. 2013b. Disponível em: norma_tecnica_georreferenciamento_imoveis_rurais_3ed.pdf (incra.gov.br)

França, L. L. S. D., Seixas, A. D., Gama, L. F., & Moraes, J. N. D. (2021). OPTIMIZED DETERMINATION OF 3D COORDINATES IN THE SURVEY OF INACCESSIBLE POINTS OF BUILDINGS-EXAMPLE OF APPLICATION IMPLEMENTED IN FREE SOFTWARE. Boletim de Ciências Geodésicas, 27. https://www.researchgate.net/publication/352817150_OPTIMIZED_DETERMINATION_OF_3D_COORDINATES_IN_THE_SURVEY_OF_INACCESSIBLE_POINTS_OF_BUILDINGS_-_EXAMPLE_OF_APPLICATION_IMPLEMENTED_IN_FREE_SOFTWARE_Determinacao_otimizada_de_coordenadas_3D_no_levantamen

Simões, D. P.; Albarici, F. L.; Borges, P. A. F. (2017). Análise comparativa das coordenadas no Sistema Geodésico Local e no Sistema Topográfico Local. R. bras. Geom., Curitiba, v. 5, n. 1, p. 062-081.

Compartilhes nas redes Sociais

ÚLTIMOS POSTS
CONHEÇA NOSSOS CURSOS
Curso drone
Python para QGIS
Sensoriamento Remoto com QGIS
Leandro França

Politica de Privacidade

FALE CONOSCO
contato@geoone.com.br

Instagram Youtube