Transformação entre SIRGAS2000, SAD69 e Córrego Alegre
O emprego de programas computacionais de SIG para a conversão de coordenadas de dados geoespaciais entre diferentes Sistemas Geodésicos de Referência (SGR) requerem uma série de cuidados. Muitos usuários por desconhecimento ou negligência acabam embutindo erros aos produtos cartográficos finais e às análises decorrentes.
Este artigo tem como objetivo servir de base na utilização no QGIS para as transformações de coordenadas dos SGR anteriormente adotados no Brasil para o sistema atual, o SIRGAS2000, utilizando como referência para validação o software ProGriD, o qual é recomendado pelo IBGE para transformação entre os SGR por modelar as distorções existentes entre as redes geodésicas clássicas através de grades no padrão NTv2.
O que é um Sistema Geodésico de Referência (SGR)?
Um Sistema Geodésico de Referência (SGR) é definido com base em um conjunto de parâmetros e convenções que buscam adaptar um elipsoide às dimensões da Terra (Borges e Elmiro, 2014), possibilitando determinar a posição de pontos em sua superfície num referencial apropriado.
Quando ocorre a materialização (ou realização) de um SGR, ou seja, a determinação de um conjunto de coordenadas de estações calculadas por técnicas de posicionamento de precisão compatível com sua finalidade (Cordini et al., 1998), cria-se uma estrutura ou rede de referência que funciona para controles horizontal e vertical necessários à localização e à representação cartográfica de um território (Borges & Elmiro, 2014; Fernandes & Nogueira, 2010).
Histórico dos SGR no Brasil
No Brasil, a materialização de um SGR é denominada de Sistema Geodésico Brasileiro (SGB) (Fernandes & Nogueira, 2010), sendo composta por redes altimétricas, planimétricas e gravimétricas. Essas redes podem ser caracterizadas por duas fases distintas: uma anterior e outra posterior ao advento da tecnologia de observação de satélites artificiais com fins de posicionamento (Sampaio et al., 2015).
Na fase anterior ao posicionamento pelo Global Navigation Satelitte System (GNSS), conhecida como clássica, as coordenas eram obtidas por determinações astronômicas, sendo comum a implantação de uma origem, estabelecida como um marco inicial para encaminhamentos de qualquer trabalho de georreferenciamento, denominada de datum (Sampaio et al., 2015), sendo definido por cinco parâmetros: vértice de origem, coordenadas, azimute, altura geoidal e elipsóide de referência (Fernandes & Nogueira, 2010).
Vale destacar que, no Brasil, o termo “datum”, designando para o ponto de origem de uma rede planimétrica ou altimétrica, não deve ser confundido como um SGR, como verificado em outros países (Cordini et al., 1998). Este termo vem gradativamente entrando em desuso devido às novas técnicas de posicionamento pelo GNSS.
Acompanhando a evolução das tecnologias de posicionamento, os produtos cartográficos existentes no país, inclusive do mapeamento sistemático sob responsabilidade do IBGE (Instituto Brasileiro de Geografia e Estatística) e da DSG (Diretoria do Serviço Geográfico), basearam-se em diferentes sistemas de referência e suas realizações (Dalazoana & Freitas, 2002).
Os produtos cartográficos nacionais, gerados em diferentes épocas, seguiram as especificações e normas do SGB vigentes, estabelecidas pelo IBGE (Fernandes & Nogueira, 2010). Deste modo, de acordo com Borges e Elmiro (2014), esses produtos foram referenciados com base em diferentes sistemas, sendo os principais: Córrego Alegre (realizações 1961 e 1970/1972), Astro Datum Chuá, South American Datum 1969 – SAD69 (realização inicial, realização 1996 e realização técnica Doppler ou GPS), e por último, o Sistema de Referência Geocêntrico para as Américas com realização na época 2000,4 (SIRGAS2000).
Segundo Pino e Firkowski (2009), os SGR mais utilizados no Brasil foram o Córrego Alegre, adotado no país da década de 50 até a década de 70, tendo como superfície de referência o Elipsoide Internacional de Hayford de 1924 e o vértice de Córrego Alegre como origem; e o sistema SAD69 que foi adotado a partir da década de 70, tendo como superfície de referência o Elipsoide Internacional de 1967 e o vértice Chuá como origem.
Com a resolução nº1/2005 do IBGE, a qual estabeleceu, a partir de 2015, o SIRGAS2000 como o único referencial planimétrico oficial do Brasil (Brito et. al., 2013; Monico et al., 2014), uma quantidade significativa de documentos cartográficos passou a ter a necessidade de transformação ou adequação a este novo referencial (Pino e Firkowski, 2009).
Transformação entre Referenciais Geodésicos
A transformação entre referenciais consiste em encontrar a posição de uma estação conhecida em um determinado sistema de referência (ou realização) em outro sistema (ou realização) e vice-versa (Monico et al., 2014; Magna Junior et al., 2009).
A coexistência de diversos SGR e suas realizações requerem modelos matemáticos para conversão de coordenadas entre eles (Monico et al., 2014; Ziggah et al., 2019).
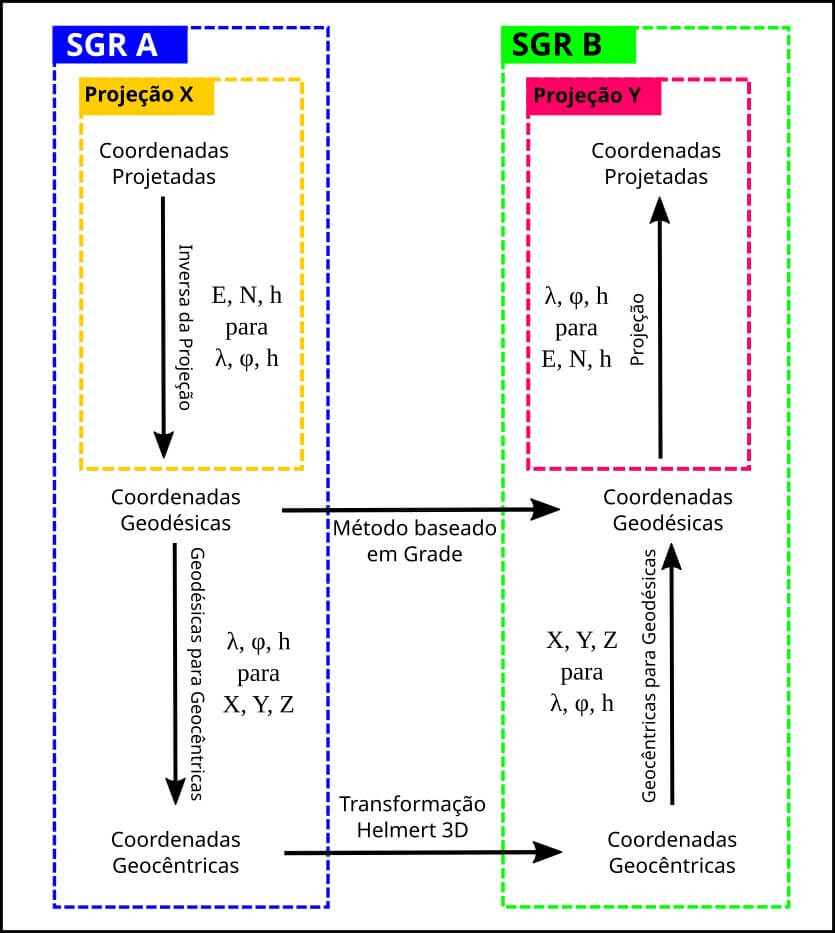
A transformação entre SGR pode ser realizada diretamente, convertendo as coordenadas geodésicas de um SGR para outro; ou indiretamente, passando as coordenadas geodésicas (λ, φ, h) para um sistema cartesiano geocêntrico (X, Y, Z), comumente conhecido como ECEF, acrônimo para Earth-Centered, Earth-Fixed (Krzyżek, 2015), em seguida realizando-se as devidas transformações geométricas nesse sistema e, por último, retornando o resultado final em coordenadas geodésicas (Figura 1).
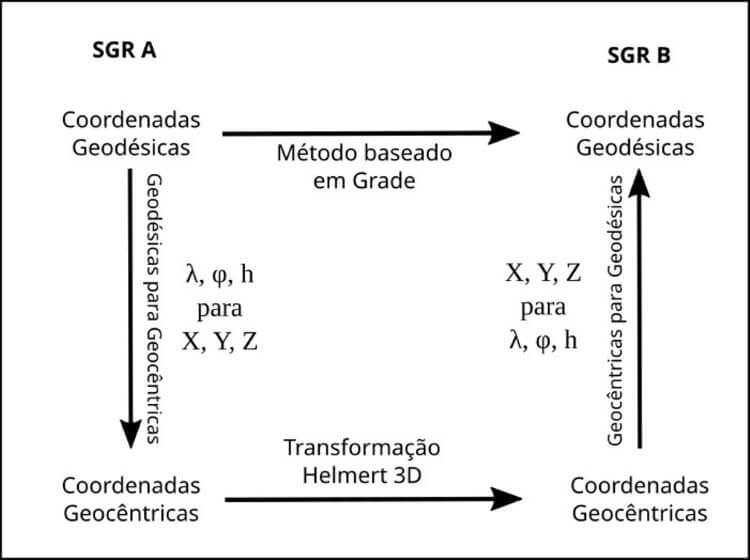
Dentre as conversões diretas, podem ser citadas a transformação de Molodensky e o método baseado em Grades (Grid-based method). Já para as conversões indiretas cita-se a transformação de Helmert e a transformação de Molodensky-Badekas (Ziggah et al., 2019).
Neste artigo, são abordadas apenas a transformação de Helmert e o Método Baseado em Grades, considerando-se que são os métodos de conversão de coordenadas adotados pelos softwares QGIS e ProGriD para a transformação entre os SGR brasileiros.
Método Baseado em Grades
Inicialmente no Brasil, para a transformação entre diferentes sistemas de referência, era normatizado, pelas Resoluções nº 22/1983 e nº 23/1989 do IBGE, a utilização das equações diferenciais simplificadas de Molodensky (Cordini et al., 1998; Monico et al., 2014; Borges & Elmiro, 2014).
No entanto, o erro passível no processo de transformação devido às distorções era negligenciado. Brito et al. (2013), por exemplo, em seu estudo na região de Santa Catarina verificou que as distorções são da ordem de 5 m quando não são modelados esses erros.
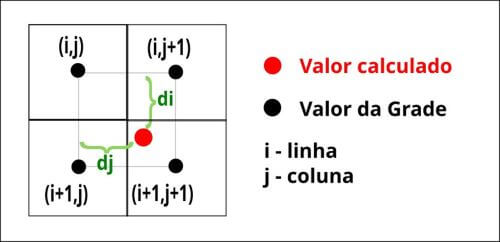
A transformação baseada em grades converte diretamente as coordenadas de um SGR para outro SGR considerando a modelagem das distorções. Deste modo, a elevada acurácia posicional da rede geodésica de referência é distribuída através da propagação das correções nos elementos da grade. Além disso, a transformação baseada em grades é computacionalmente mais eficiente, realizando apenas uma interpolação bilinear (Garnero, 2013) entre os quatro elementos mais próximos da grade que enquadram as coordenadas do ponto a ser transformado.
A Figura 2 ilustra a aplicação da interpolação bilinear, cujo cálculo dos novos valores das coordenadas V=(Vx, Vy) é determinado pela Equação 1, a partir dos valores da grade de transformação T=(Tx(i,j), Ty(i,j)).
(1) ![]()
Segundo Garnero (2013), métodos baseados em grade vêm sendo empregados nos Estados Unidos e Canadá para conversão de coordenadas entre o NAD 1927 e NAD 1983. Austrália e Nova Zelândia também adotaram essa sistemática para conversão entre o AGD 1966 e AGD 1984 e entre NZGD 1949 e NZGD 2000, respectivamente.
ProGriD para transformação de coordenadas
No Brasil, a transformação entre SGR pelo método baseado em grades para a modelagem das distorções foi amplamente difundido através do lançamento do ProGriD a partir de dezembro de 2008 (Magna Junior et al., 2014).
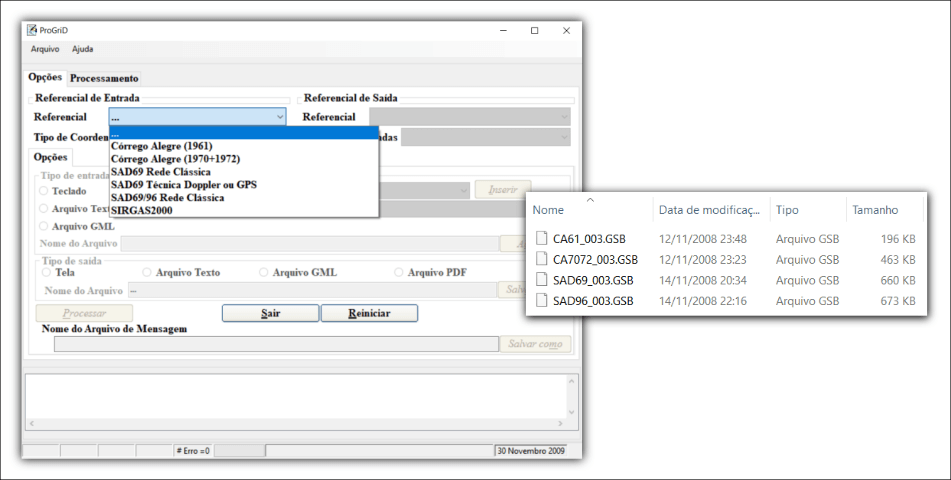
O ProGriD é uma ferramenta computacional que realiza transformações de coordenadas entre as realizações do Córrego Alegre, SAD 69 e SIRGAS2000. Este software contém os deslocamentos (shifts) entre os pares de realizações das redes geodésicas (reference frames) armazenados em arquivos no formato National Transformation version 2 (NTv2) (Santos et al., 2012).
As grades de transformação NTv2 utilizadas no ProGriD são geradas a partir de estações homólogas considerando as seguintes materializações: Córrego Alegre (1961), Córrego Alegre (1970+1972), SAD69 Rede Clássica e SAD69/96 Rede Clássica (Magna Junior et al., 2014).
De acordo com Magna Junior et al. (2009), essas grades de transformação foram calculadas pela interpolação das distorções das estações mais próximas considerando a ponderação pela distância e direção relativa entre eles, conhecida como método de Shepard.
Os arquivos de grades NTv2, no ProGriD, estão na extensão Grid Shift Binary (GSB), podendo ser acessado no sistema operacional Windows em C:\Arquivos de Programas\Progrid\GridFiles (Brito et al., 2013).
Santos et al. (2012) explica que as redes de natureza distintas (clássicas e por GNSS) são tratadas de forma diferente no ProGriD. As redes clássicas se relacionam com o SIRGAS2000 pelos arquivos GSB, modelando suas distorções. Já para a rede geodésica SAD69, que utiliza técnicas Doppler ou GPS, são utilizados três parâmetros de translação (dx, dy, dz) que se relacionam com o SIRGAS2000 através da transformação de Helmert (Oliveira et al., 2009).
A Figura 3 apresenta, à esquerda, os SGR implementados no ProGriD e à direita os arquivos GSB de conversão dos sistemas clássicos para SIRGAS2000.
O ProGriD também possui a vantagem de lidar com as incertezas associadas às transformações (Santos et al., 2012), além de permitir se trabalhar com coordenadas projetadas (E,N,h) no sistema UTM (Collischonn et al., 2015). Embora não seja exatamente uma desvantagem, o ProGriD não trabalha com pontos fora da área predefinida para o Brasil continental (Santos et al., 2012).
Transformação de coordenadas no QGIS com a biblioteca PROJ
O QGIS é um é um software livre de código aberto e multiplataforma que provê a visualização, edição e análise de dados georreferenciados, permitindo ao usuário criar mapas com várias camadas de informação em diferentes sistemas de coordenadas.
O termo Sistema Geodésico de Referência (SGR) propriamente dito não é comum no QGIS. Neste software, é mais utilizado o termo Sistema de Referência de Coordenadas (SRC). Quando um SRC é do tipo geográfico, ou seja, é um sistema de coordenadas curvilíneas cuja unidade é graus decimais, então pode-se assumir que se trata de um SGR.
De acordo com a equipe de desenvolvedores (QGIS Development Team, 2019), o QGIS reconhece aproximadamente 7.000 SRC definidos pelo European Petroleum Search Group (EPSG) e pelo Institut Geographique National de France (IGNF), utilizando-se da biblioteca de projeções “Proj.4”.
A biblioteca PROJ, anteriormente conhecida com Proj.4, é um projeto iniciado por Gerald I. Evenden em 1983 como a implementação dos resultados do trabalho de John Snyder, denominado inicialmente de “Map projections used by the U.S. Geological Survey” em 1982 e depois de “Map Projections: A working manual” em 1987 (Evers & Knudsen, 2017). Esse projeto possibilitou a conexão entre diferentes SRC, mesmo que baseada inicialmente apenas em formulações matemáticas.
Hoje, com mais de 35 anos, o Proj.4 fornece parâmetros de conversão de coordenadas para praticamente todos os programas que lidam com dados geoespaciais. Além disso, atualmente conta com técnicas de transformações de coordenadas geodésicas de alta precisão baseadas em estruturas capazes de considerar até mesmo a relação espaço-temporal das coordenadas (Evers & Knudsen, 2017).
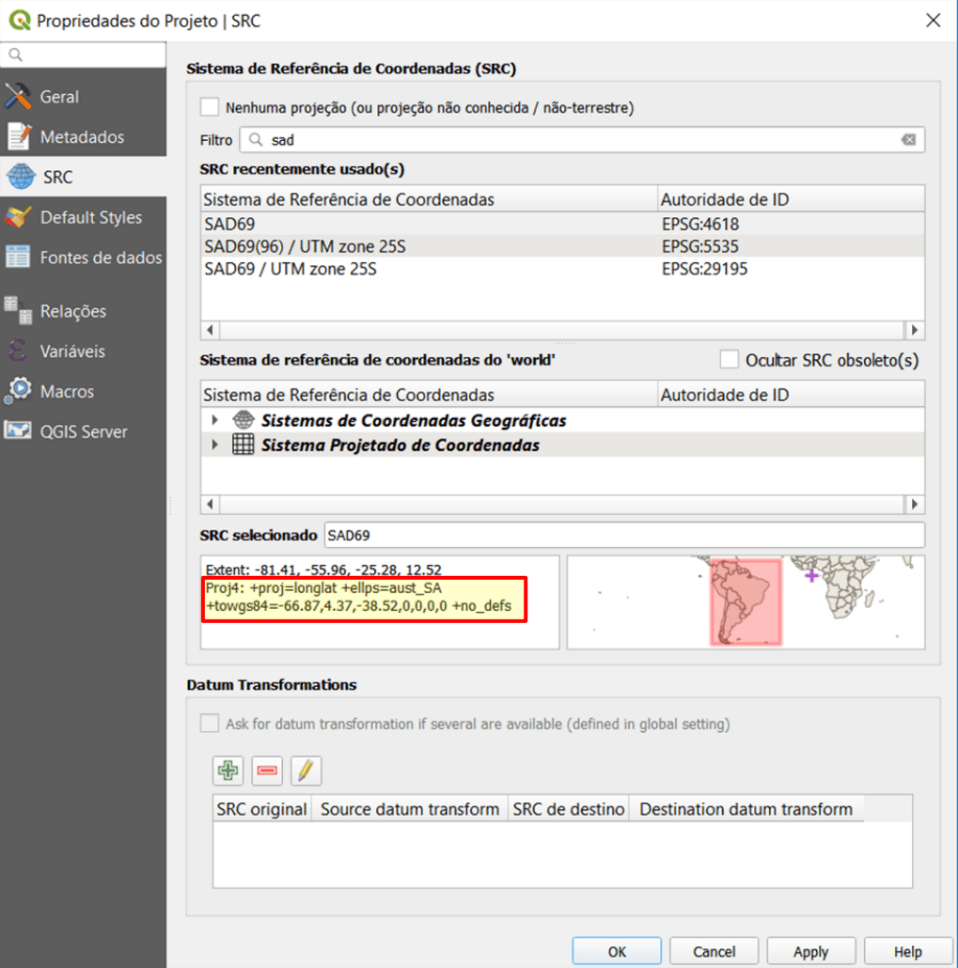
As projeções e transformações do Proj.4 são expressas como “proj-strings”. No QGIS, a proj-string é identificada nas configurações do SRC, sendo exemplificada na Figura 4, onde são identificados os parâmetros de transformação do SAD69 em relação ao World Geodetic System 1984 (WGS84).
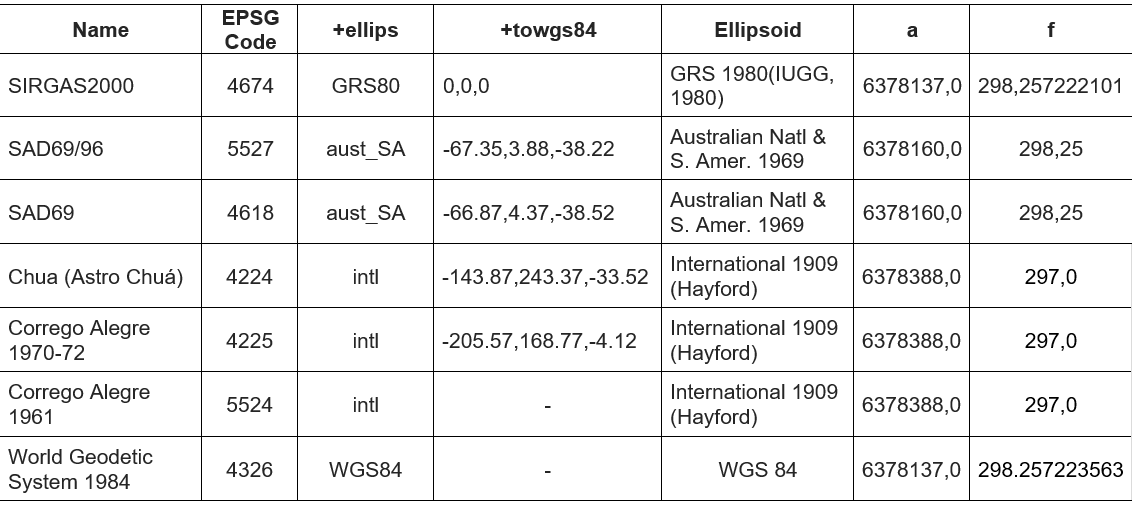
Para a transformação entre os SGR brasileiros, as configurações do Proj.4 do QGIS utilizam os parâmetros apresentados na Tabela 1, onde +ellps e +towgs84 correspondem ao elipsoide utilizado e os parâmetros de transformação de Helmert, respectivamente.
Tabela 1: Parâmetros de alguns SGR utilizados no QGIS
Transformação de Helmert 3D
Para todos os casos da Tabela 1, as coordenadas geodésicas são convertidas em coordenadas ECEF (X,Y,Z) em um referencial “A”, em seguida é realizada a transformação de Helmert com 7 parâmetros (Equação 2), considerando-se 3 translações (T), 1 fator de escala (s) e 3 rotações (R), e desprezando-se as taxas de variação (velocidades) desses parâmetros (Sapucci & Monico, 2000). Após a transformação entre os sistemas geocêntricos, as coordenadas ECEF no referencial “B” são convertidas de volta para coordenadas geodésicas.
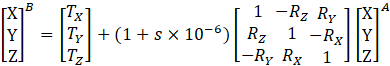 (2)
(2)
Da Tabela 1, observa-se também que os parâmetros de transformação entre SIRGAS2000 e WGS84 são nulos, pois, além de ambos utilizarem o mesmo elipsoide Geodetic Reference System 1980 (GRS80) (Sapucci & Monico, 2000), o SIRGAS2000 é equivalente ao WGS84 na semana GPS G1150, para efeitos práticos da cartografia (Dalazoana & Freitas, 2002).
Do exposto sobre QGIS e Proj.4, vale salientar a ampla possibilidade de se configurar novos SRC personalizados utilizando-se de simples definições de parâmetros através de proj-string, muito bem documentados pelo contribuidores do projeto Proj.4 através do endereço eletrônico https://proj.org/ (PROJ, 2019).
Vantagens de transformação de coordenadas no QGIS
O QGIS, além de contar com um elevado número de SRC já implementados e a possibilidade de criação de novas transformações personalizados pelo Proj.4, a grande praticidade de transformação entre os SGR tanto para dados vetoriais quanto matriciais, onde os resultados da conversão podem ser comparados pela inspeção visual em tela entre as camadas e feições de referência.
Em relação ao método baseado em grades, o Proj.4 incluiu suas funcionalidades no início dos anos 2000 (Evers & Knudsen, 2017), possibilitando que muitos softwares de SIG também lidem com NTv2 (Santos et al., 2012; Garnero, 2013; Monico et al., 2014). Deste modo, desde que configurado os arquivos GSB no QGIS, torna-se possível realizar transformações diretas entre SGR que modelam as distorções com resultados análogos ao ProGriD.
Método baseado em Grades no QGIS
Os mesmos arquivos de grade NTv2 (formato GSB) do ProGriD, quando configurados no QGIS, chegam a resultados iguais. Para isso, foi utilizada a criação dos sistemas de coordenadas personalizados com as Proj-strings apresentadas na Tabela 2.
Tabela 2: Proj strings para configuração de SRC com os arquivos de grade NTv2.

Ressalta-se que, para que as configurações apresentadas funcionem corretamente, os arquivos de grades NTv2 devem ser copiados para a pasta C:\Program Files\QGIS 3.22\share\proj, neste caso para os usuários do Windows.
Problemas atrelados às transformações de Referenciais
Essas transformações não é um problema trivial que pode ser resolvido no espaço abstrato através de uma função matemática (Magna Junior et al., 2009). A complexidade da transformação está relacionada à existência de erros de distorções e de outras influências nas realizações dos sistemas, causados, principalmente, pela utilização de diferentes equipamentos, além das estratégias de processamento e integração não consistente dos dados coletados, dentre outros fatores.
Magna Junior et al. (2009) também afirmam que para o aproveitamento de produtos analógicos e digitais já existentes nos antigos referenciais, são necessárias metodologias para conversão de coordenadas que minimizem as distorções entre as diferentes realizações e isso vem sendo objeto de várias pesquisas, podendo ser citados: Oliveira et al. (2009), Magna Junior et al. (2009), Santos et al. (2012), Magna Junior et al. (2014) e Ziggah et al. (2019).
Apesar de todos os esforços em modelar as distorções entre os diferentes SGR, por desconhecimento ou comodidade, muitas instituições e empresas acabam aplicando basicamente as transformações implementadas em softwares de Sistema de Informações Geográficas (SIG), sem qualquer preocupação com as distorções inerentes às observações não homogêneas (Brito et al., 2013).
E as projeções cartográficas, onde entram?
A projeção cartográfica aplica um modelo matemático às coordenadas geodésicas para que as coordenadas curvilíneas (angulares) passem a ser representadas em uma superfície desenvolvível em um plano (clique aqui para saber mais sobre projeções).
A Figura 5 mostra o fluxo mais comum de transformação de coordenadas de uma Projeção X, no SGR A, para uma outra projeção Y, no SGR B. Observa-se que as coordenadas projetadas são transformadas em coordenadas Geodésicas, as quais podem ser transformadas tanto pelo método baseado em grade quanto por Helmert.
Aprenda na Prática como realizar todas essas transformações no QGIS com dicas incríveis
Quer aprender na prática Cartografia no QGIS?
Então se torne um Geonista clicando no link abaixo:
Quer dominar todas as configurações do QGIS?
Então conheça o curso QGIS: Teoria e Prática:

Referências:
BORGES, ANDRE FERREIRA; ELMIRO, MARCOS ANTÔNIO TIMBÓ. OS DIFERENTES SISTEMAS GEODÉSICOS DE REFERÊNCIA E SUAS DISCREPÂNCIAS NA REGIÃO DE NOVA LIMA-MG. V Simpósio Brasileiro de Ciências Geodésicas e Tecnologias da Geoinformação: Recife, PE, Anais, p. 537-546, 2014.
Brito, B. V., da Silva, P. V., da Silva, J. O., & Júnior, J. P. M. Mudança de referenciais geodésicos utilizando grades de transformação integradas em programas computacionais SIG. Anais XVI Simpósio Brasileiro de Sensoriamento Remoto – SBSR, Foz do Iguaçu, PR, Brasil, 13 a 18 de abril de 2013, INPE.
Brasil. 1984. Decreto nº 89.817 de 20 de Junho de 1984. Normas Técnicas da Cartografia Nacional.
Collischonn, C., de Lima, E. M., Ruiz, L. F. C., Araujo, T. D., & Matsuoka, M. T. Posicionamento GNSS: Comparação entre coordenadas oficiais de estações da RBMC e as obtidas por PPP e posicionamento relativo e ajustamento. Anais XVII Simpósio Brasileiro de Sensoriamento Remoto – SBSR, João Pessoa-PB, Brasil, 25 a 29 de abril de 2015, INPE.
Cordini, J., GARNÉS, S. J. D. A., MORAES, C. V. D., & Nadal, C. A. (1998). Transformações de Referenciais Geodésicos. COBRAC 98 – Congresso Brasileiro de Cadastro Técnico Multifinalitário – UFSC – Florianópolis – 18 a 22 de Outubro de 1998.
DALAZOANA, Regiane; DE FREITAS, Sílvio Rogério Correia. Efeitos na Cartografia devido a evolução do sistema geodésico brasileiro e adoção de um referencial geocêntrico. Revista Brasileira de Cartografia, n. 54, 2002.
DSG. Diretoria do Serviço Geográfico. 2015. Norma da Especificação Técnica para Aquisição de Dados Geoespaciais Vetoriais de Defesa da Força Terrestre – ET-ADGV. 1ª Edição.
Evers, K. and Knudsen, T. Transformation pipelines for PROJ.4. In FIG Working Week 2017 Proceedings. Helsinki, Finland, 2017. URL: http://www.fig.net/resources/proceedings/fig_proceedings/fig2017/papers/iss6b/ISS6B_evers_knudsen_9156.pdf.
FERNANDES, Vivian de Oliveira; NOGUEIRA, Ruth Emilia. Consequências da mudança de datum na representação cartográfica direcionada para ambiente SIG. 2010. Portal de Cartografia. Londrina, v.3, n.1, 2010. 5-61.
FRANÇA, Leandro Luiz Silva de; SILVA, Luiz Felipe Coutinho Ferreira da. Comparison between the Double Buffer Method and the Equivalent Rectangle Method for the quantification of discrepancies between linear features. Boletim de Ciências Geodésicas, v. 24, n. 3, p. 300-317, 2018.
FRANÇA, L.L. S.,PENHA, A. L. T. and CARVALHO,J.A. B. Comparison Between Absolute and Relative Positional Accuracy Assessment -A Case Study Applied to Digital Elevation Models. Bulletin of Geodetic Sciences, 25(1): e2019003, 2019.
GARNERO, Gabriele. Use of NTv2 transformation grids in engineering applications. Earth Science Informatics, v. 7, n. 2, p. 139-145, 2014.
IBGE. ProGriD. Avalailable in: https://ww2.ibge.gov.br/home/geociencias/geodesia/param_transf/default_param_transf.shtm
JÚNIOR, JOÃO PAULO MAGNA; CAMARGO, PAULO DE OLIVEIRA; GALO, MAURÍCIO. Modelagem de distorções entre SAD 69 e SIRGAS 2000 pelo método de Shepard e grades regulares. Boletim de Ciências Geodésicas, v. 15, n. 3, 2009.
JÚNIOR, João Paulo Magna; CAMARGO, Paulo De Oliveira; GALO, Maurício. Transformação de coordenadas com modelagem de distorções entre SAD69 e SIRGAS2000 com o uso de THIN-PLATE SPLINES. Boletim de Ciências Geodésicas, v. 20, n. 1, 2014.
KRZYŻEK, Robert; SKORUPA, Bogdan. The influence of application a simplified transformation model between reference frames ECEF and ECI onto prediction accuracy of position and velocity of GLONASS satellites. Reports on Geodesy and Geoinformatics, v. 99, n. 1, p. 19-27, 2015.
Monico, J. F. G., Camargo, P. D. O., Galo, M., de Oliveira, L. C., Junior, J. P. M., Rabaco, L. M., … & Obregon, J. R. (2014). INVESTIGATION THE ACCURACY OF THE TRANSPETRO GEODETIC NETWORK AND ITS TRANSFORMATION TO SIRGAS2000. Anais da Rio Oil & Gas Expo and Conference 2014. 15 a 18 de setembro de 2014, no Rio de Janeiro.
Oliveira, L. C., Santos, M. C., Nievinski, F. G., Leandro, R. F., Costa, S. M., Santos, M. F., … & Silva, C. U. (2009). Searching for the optimal relationships between SIRGAS2000, South American Datum of 1969 and Córrego Alegre in Brazil. In Observing our Changing Earth (pp. 71-79). Springer, Berlin, Heidelberg.
OSGEO. 2014. Link: https://wiki.osgeo.org/wiki/Brazilian_Coordinate_Reference_Systems
PINO, L. M., & FIRKOWSKI, H. (2009). Avaliação de modelos de transformação bidimensional para a compatibilização de bases cartográficas associadas a diversos sistemas geodésicos de referência. Boletim de Ciências Geodésicas, 15(2).
PROJ contributors (2019). PROJ coordinate transformation software library. Open Source Geospatial Foundation. URL https://proj.org/.
QGIS Development Team, 2019. Working with projections. Open Source Geospatial Foundation. Available in:
https://docs.qgis.org/3.4/en/docs/user_manual/working_with_projections/working_with_projections.html. Accessed in: June 13, 2019.
Sampaio, A. C. F., Sampaio, A. D. Á. M., Silva, T. P., & Borges, W. C. DATUM CÓRREGO ALEGRE: MONUMENTO HISTÓRICO DA CARTOGRAFIA BRASILEIRA. Atas do VI Simpósio Luso-Brasileiro de Cartografia Histórica, 4 a 7 de Novembro de 2015. Braga, Portugal.
Santos, M. F., Santos, M. C., Oliveira, L. C., Costa, S. A., Azevedo, J. B., & Galo, M. PROGRID: the transformation package for the adoption of SIRGAS2000 in Brazil. In: Geodesy for Planet Earth. Springer, Berlin, Heidelberg, 2012. p. 869-875.
SAPUCCI, L. F.; MONICO, J. F. G. Transformação de Helmert generalizada no posicionamento de alta precisão: fundamentação teórica e exemplificações. Revista Brasileira de Geofísica, p. 161-172, 2000.
ZIGGAH, Yao Yevenyo et al. Coordinate Transformation between Global and Local Datums Based on Artificial Neural Network with K-Fold Cross-Validation: A Case Study, Ghana. Earth Sciences Research Journal, v. 23, n. 1, p. 67-77, 2019.




















