Projeções customizadas: UTM, RTM e LTM no QGIS
As grandes demandas de mapeamento para a geração ou atualização de bases cartográficas do Cadastro Técnico Multifinalitário (CTM) têm sido um desafio para muitos municípios brasileiros. Umas das grandes dificuldades enfrentadas se refere a qual projeção cartográfica deve ser utilizada na geração de plantas cadastrais para o cálculo exato de medidas de área e perímetro dos imóveis.
É muito comum empresas de engenharia adotarem uma das projeções do sistema Universal Transversa de Mercator (UTM) na entrega dos seus produtos cartográficos, devido à facilidade de integração dos dados com outros sistemas ou softwares. Entretanto, também não é raro que a extensão do município esteja entre dois fusos, como é o caso do exemplo abaixo, para o município de Caruaru-PE.
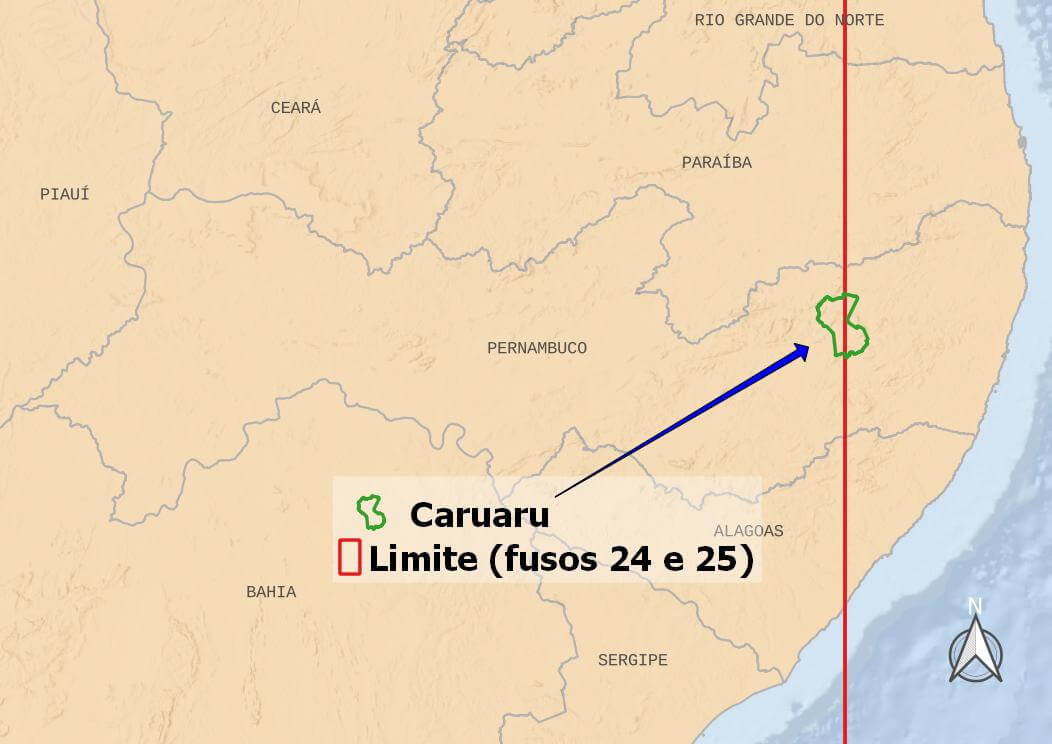
Nesse caso, adotando-se qualquer um dos fusos, parte do município ficará “de fora” da área do fuso e, inevitavelmente, implicará em maiores distorções nos cálculos realizados nesse sistema.
O objetivo deste Post, é apresentar algumas alternativas que podem ser adotadas pelos municípios para a padronização dos trabalhos de engenharia e amarração dos projetos a um sistema único de coordenadas.
Quando adotar uma projeção personalizada para uma base cadastral?
Como mencionado anteriormente, uma projeção personalizada deve ser utilizada sempre que:
◼️ as projeções predefinidas não se adequarem à extensão da região a ser mapeada;
◼️ deseja-se minimizar as distorções (área, escala ou forma) causadas pela projeção.
Diversas projeções cartográficas personalizadas poderiam ser adotadas no mapeamento estadual e municipal aqui no Brasil.
Fazendo um comparativo com os Estados Unidos, lá existe o Sistema Coordenadas chamado de “State Plane”, composto de 125 projeções diferentes, para simplificar os métodos de levantamento topográfico em sistemas cartesianos XY mais próximo ao “plano”.
Verifica-se que maior parte das zonas do State Plane tomam por base ou a projeção Transversa de Mercator ou a Projeção Cônica Conforme de Lambert. O mapa abaixo apresenta as projeções do sistema de coordenadas State Plane.
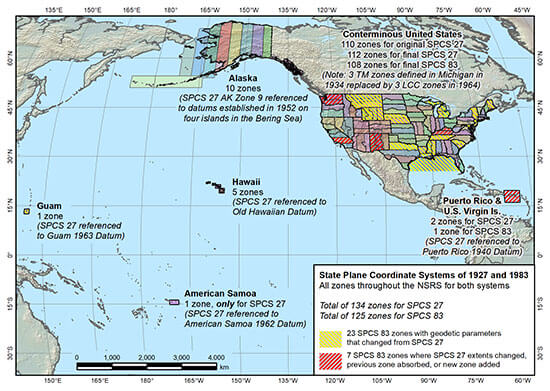
A importância de se adotar um sistema de coordenadas plano retangulares está atrelada à necessidade de se “amarrar” todos os serviços topográficos de cadastro (infraestrutura, fundiário, registros públicos, imobiliários, fiscais etc.), para projetos, locações e gerenciamento de obras públicas e particulares, inclusive as built (Holler, 2009).
No Brasil, muitos municípios ainda não possuem um sistema único de coordenadas definido em lei, sendo muito comum trabalharem apenas com o Sistema de Projeção UTM, mesmo verificando-se a necessidade de adotar uma projeção personalizada, de preferência, em Regional Transverso de Mercator (RTM) ou em Local Transverso de Mercator (LTM).
O que é uma projeção cartográfica e suas implicações?
Projeção cartográfica consiste na técnica empregada para representar uma superfície curva em outra superfície que permita o seu desenvolvimento em 2D, ou seja, no plano para representação em um mapa, carta ou planta topográfica.
Embora existam modelos matemáticos (esféricos e elipsoidais) para tentar representar a superfície real da Terra, a correspondência dos pontos dessa superfície no mapa não é exata, ou seja, medidas lineares e angulares sofrem distorção.
A solução encontrada, é eleger alguma área da superfície e então minimizar os efeitos de distorção nessa região. Dentro desta lógica, são imaginadas três superfícies de projeção: cilíndrica, cônica ou plana (azimutal).
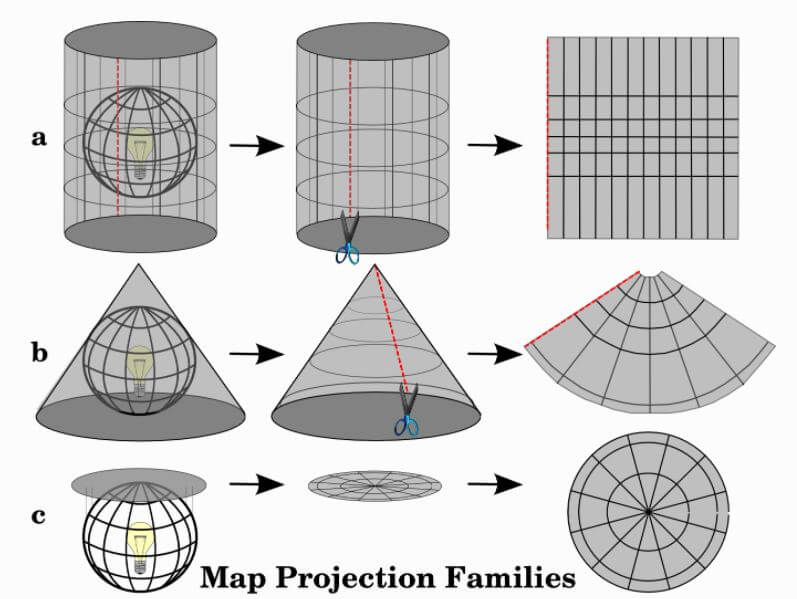
Ressalta-se que, mesmo adotando uma projeção mais adequada à região, não é possível eliminar todos os efeitos de distorção (forma, distância, área). Geralmente as projeções eliminam um dos efeitos, podendo ser classificadas de acordo com a distorção eliminada: conforme, equidistante, equivalente ou afiláticas (Nazareno, 2009).
UTM para o mapeamento sistemático
O sistema UTM é adotado no mapeamento sistemático de todo o território brasileiro na produção de cartas topográficas, principalmente, pela DSG e IBGE.
Em alguns casos, o sistema UTM não é a melhor opção para projeções de bases cadastrais municipais, cuja extensão territorial não segue um padrão sistemático e as distorções podem influenciar em medições e interferir em projetos de engenharia.
Vamos explorar agora o que vem a ser a Projeção Transversa de Mercator e como ela pode ser adaptada para o mapeamento cadastral.
Projeção Transversa de Mercator
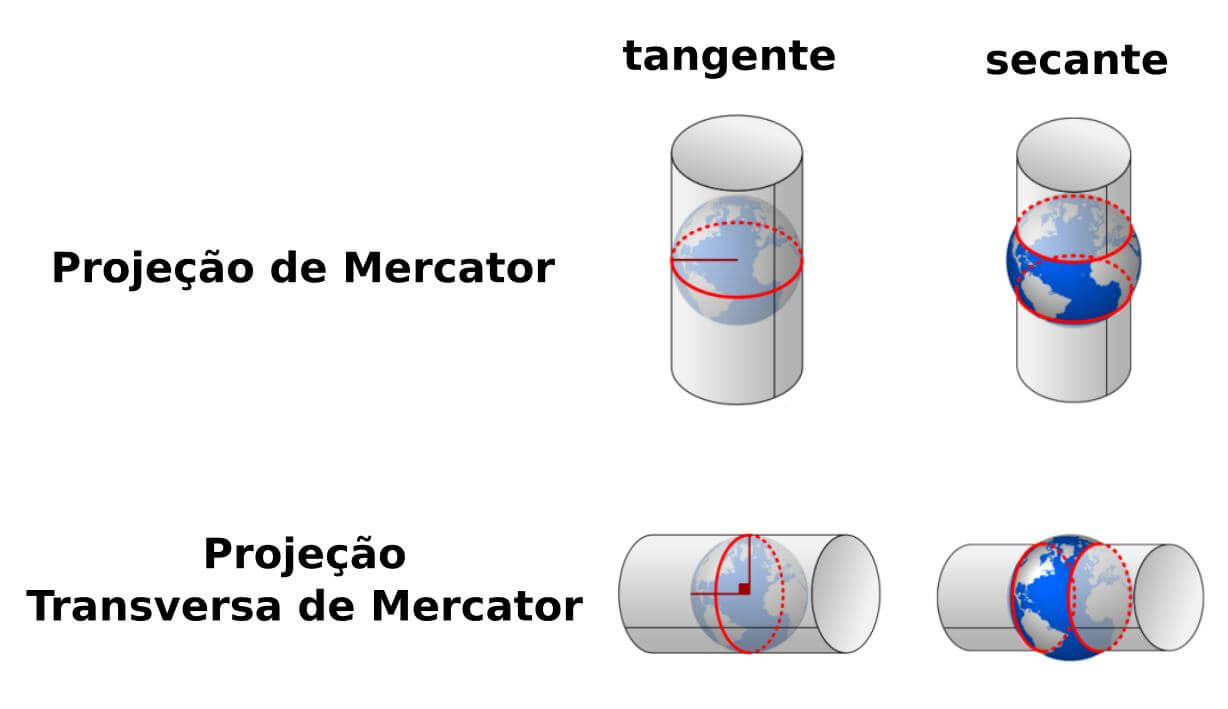
A projeção de Mercador é uma projeção conforme, que utiliza um cilindro tangente ou secante a esfera/elipsoide no equador, onde, nesta linha, não há distorção de escala.
Já a projeção Transversa de Mercator também conhecida como projeção Conforme de Lambert-Gauss é uma variante da primeira, onde a tangência se dá em um meridiano.
Entendendo o sistema de projeção UTM (Universal Transversa de Mercator)
Desenvolvido inicialmente por Gauss-Tardi (Nazareno, 2009), este sistema adota o elipsoide de revolução para modelar a superfície da Terra, sendo projetada em um cilindro transverso e secante.
Entre as duas grandes guerras, este sistema de projeção foi adotado para a confecção de cartas militares, passando a ter a denominação atual de Universal Transverso de Mercator (UTM) logo após, em 1950.
Para evitar distorções muito grandes, o mundo foi dividido em 60 cilindros, abrangendo cada um deles, uma amplitude de 6° em longitude. A cada uma das 60 faixas de 6°, chamou-se de fuso.
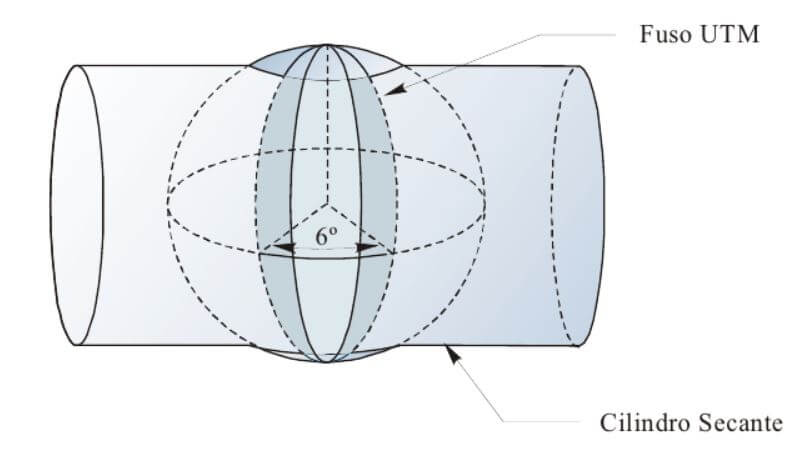
A posição desses cilindros foi convencionada, iniciando-se no anti-meridiano de Greenwich e seguindo a contagem dos fusos de oeste para leste.
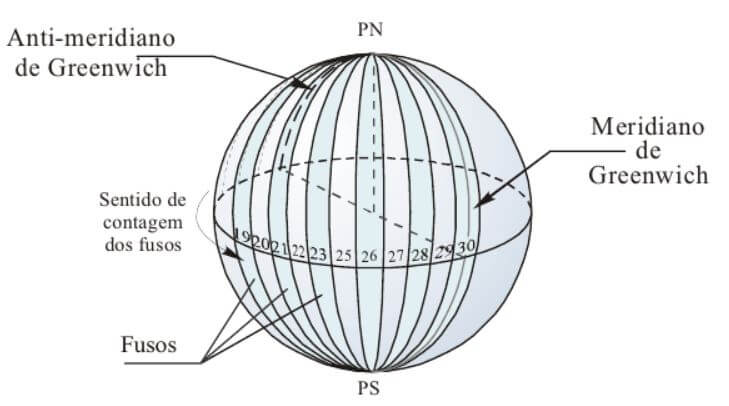
No meridiano central, o fator de escala/deformação é igual a k0 = 0,9996.
A equação que calcula o número do fuso em função da longitude λ é dada por:
(1) ![]()
Por que não utilizar o termo “projeção UTM”?
Baseado no que vimos até agora, não é adequado falar que UTM é uma projeção!
O termo UTM, na verdade, se refere a um conjunto de projeções, mais especificamente 120 projeções, duas para cada fuso (hemisfério norte e sul), onde a projeção é a Transversa de Mercator (ou Conforme de Gauss), variando-se os parâmetros: Meridiano Central, falso Norte e falso Leste.
Quando usar uma projeção RTM ou LTM?
Outras variações da projeção Transversa de Mercator podem ser observadas, podendo elas ser enquadradas em RTM (Regional Transverso de Mercator) e LTM (Local Transverso de Mercator), diferenciando-se principalmente pela amplitude do fuso e constante de distorção k0 utilizada.
A Tabela abaixo faz um comparativo entre os parâmetros que definem as projeções em UTM, RTM e LTM.
Tabela 1: Comparativo entre as projeções em UTM, RTM e LTM
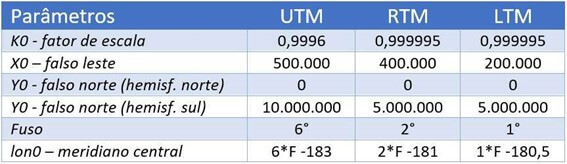
No caso da tabela acima as projeções obedecem a um mapeamento sistemático, mas nada impede de se definir o valor do meridiano central, de tal forma que esteja centralizado na região a ser mapeada. É o que veremos a seguir!
Como configurar uma projeção personalizada no QGIS?
O QGIS faz uso da biblioteca PROJ (antigamente conhecida como PROJ4) para a transformação de coordenadas geodésicas ou projetadas entre diferentes SRC. Hoje, o PROJ é um projeto open source da OSGeo e tem catalogado centenas de diferentes projeções, sendo uma biblioteca robusta e utilizada por diversos softwares de SIG, como o QGIS.
Embora o QGIS ainda não possua as projeções nos sistemas RTM e LTM, ele permite a criação dessas projeções, seja a partir de Well Known Text (WKT) ou da própria sentença PROJ.
Criação de SRC customizado a partir de WKT
Para criar sua própria projeção customizada, primeiro acesse o menu Configurações > Personalizar projeções… e você verá a seguinte caixa de diálogo:
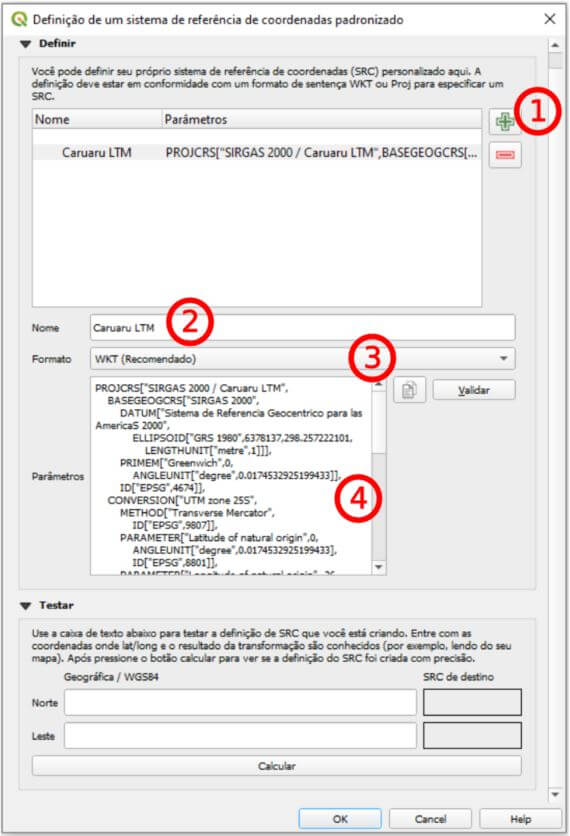
- Clique no botão verde para adicionar um novo SRC.
- Entre com o nome do SRC.
- Em formato, escolha WKT.
- Adicione a seguinte string para definir uma projeção Transversa de Mercator com os parâmetros do LTM:
PROJCRS["SIRGAS 2000 / Caruaru LTM", BASEGEOGCRS["SIRGAS 2000", DATUM["Sistema de Referencia Geocentrico para las AmericaS 2000", ELLIPSOID["GRS 1980",6378137,298.257222101, LENGTHUNIT["metre",1]]], PRIMEM["Greenwich",0, ANGLEUNIT["degree",0.0174532925199433]], ID["EPSG",4674]], CONVERSION["UTM zone 25S", METHOD["Transverse Mercator", ID["EPSG",9807]], PARAMETER["Latitude of natural origin",0, ANGLEUNIT["degree",0.0174532925199433], ID["EPSG",8801]], PARAMETER["Longitude of natural origin",-36, ANGLEUNIT["degree",0.0174532925199433], ID["EPSG",8802]], PARAMETER["Scale factor at natural origin",0.999995, SCALEUNIT["unity",1], ID["EPSG",8805]], PARAMETER["False easting",200000, LENGTHUNIT["metre",1], ID["EPSG",8806]], PARAMETER["False northing",5000000, LENGTHUNIT["metre",1], ID["EPSG",8807]]], CS[Cartesian,2], AXIS["(E)",east, ORDER[1], LENGTHUNIT["metre",1]], AXIS["(N)",north, ORDER[2], LENGTHUNIT["metre",1]], USAGE[ SCOPE["Engineering survey, topographic mapping."], AREA["Caruaru city - Pernambuco."], BBOX[-8.3987819749999630,-36.1806799069999556,-7.9763393489999430,-35.8515568659999531]]]
Em seguida clique em OK e defina o seu projeto para esse novo SRC.
Criação de SRC customizado a partir de WKT (Well Known Text)
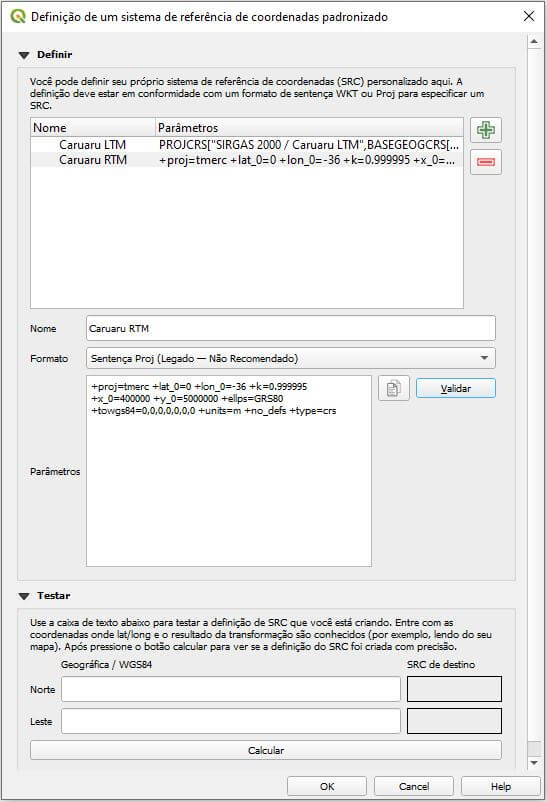
Embora não seja recomendado, mas bastante utilizada nas versões antigas do QGIS, um SRC pode ser criado de forma personalizada utilizando-se uma sentença Proj.
No exemplo abaixo, estamos criando uma projeção em RTM para a mesma região de Caruaru-PE com a seguinte sentença:
+proj=tmerc +lat_0=0 +lon_0=-36 +k=0.999995 +x_0=400000 +y_0=5000000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs
Nesse último caso, algumas informações sobre o SRC acabam sendo omitidas como o BBOX e descrição do sistema geodésico.
Assista nossa aula e veja o resultado comparativo desses sistemas de referências de coordenadas (SRC) na prática, no QGIS:
Como uma Prefeitura Municipal pode definir uma Projeção Personalizada em Lei?
Primeiro, deve-se elaborar um parecer por um comitê de cartografia, com objetivo de avaliar e identificar os melhores parâmetros de projeção a ser utilizado no município, sendo o Sistema Geodésico de Referência oficial, o SIRGAS 2000.
Em seguida, um Portaria deve ser criada estabelecendo a obrigatoriedade de apresentação das plantas topográficas de glebas e imóveis, bem como projetos arquitetônicos ou de engenharia e infraestrutura sejam georreferenciadas neste SRC.
Aprenda mais sobre Cartografia e QGIS nos nossos cursos:
Referências:
Holler, W. Além das coordenadas UTM. MundoGEO. 2009. Disponível em: https://mundogeo.com/2009/01/06/alem-das-coordenadas-utm/
Nazareno, N. Cartografia Geral: Notas de aula. 2009.
NOAA. National Geodetic Survey. State Plane Coordinate System (SPCS). Disponível em: https://geodesy.noaa.gov/SPCS/
PROJ contributors (2020). PROJ coordinate transformation software library. Open Source Geospatial Foundation. URL https://proj.org/.
QGIG.org. Coordinate Reference Systems. Disponível em: https://docs.qgis.org/3.16/en/docs/gentle_gis_introduction/coordinate_reference_systems.html
USP. Escola Politécnica da Universidade de São Paulo. Laboratório de Topografia e Geodesia. Notas de aula. Disponível em: https://edisciplinas.usp.br/pluginfile.php/4530334/mod_resource/content/10/PTR5003%20-%20Proje%C3%A7%C3%A3o%20UTM%20v2019.pdf
https://docs.qgis.org/3.16/en/docs/training_manual/vector_analysis/reproject_transform.html
https://proj.org/operations/projections/tmerc.html
https://docs.qgis.org/3.16/en/docs/gentle_gis_introduction/coordinate_reference_systems.html




















