Pesquisar
Close this search box.
Instagram Youtube

Categoria: , ,

Cálculo de Azimutes e Distâncias

Topografia - Azimute e Distância

Azimutes e Distâncias: Fundamentos para a Topografia

 

A topografia desempenha um papel crucial em diversos setores, desde a cartografia até a construção civil e agricultura. Para profissionais que trabalham nesse campo, entender os conceitos de azimutes e distâncias é fundamental, uma vez que esses valores são a base para a realização de medições precisas.

Neste artigo, abordaremos a importância de conhecer e calcular azimutes e distâncias na topografia, apresentando definições, fórmulas e exemplos de aplicações com coordenadas no sistema UTM (Universal Transverse Mercator), através do cálculo analítico, bem como na prática com o QGIS ou usando Python.

 

Cálculo analítico de Azimutes e Distâncias

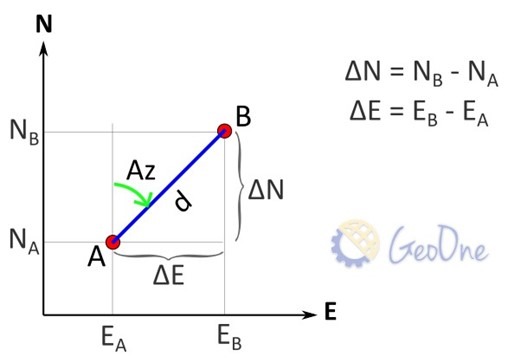
Dado dois pontos A e B de coordenadas A = (EA, NA) e B = (EB, NB)

Azimute e distância

Distâncias: A distância (d) entre esses dois pontos é a magnitude do deslocamento entre eles, medida geralmente em metros. A distância pode ser calculada utilizando o teorema de Pitágoras, como mostrado abaixo:

(1)   \begin{equation*} \mathbf{d}=\sqrt{\Delta E^2+\Delta N^2} \end{equation*}

 

Azimutes: O azimute é a direção em que um ponto se encontra em relação a outro, medido em relação ao norte. Na topografia, os azimutes são expressos em graus, medidos no sentido horário a partir do Norte. Para calcular azimutes, usamos fórmulas trigonométricas que levam em consideração as coordenadas dos pontos de origem e destino, como por exemplo do ponto A para o ponto B.

 

Azimute (Az):

(2)   \begin{equation*} A z=\arctan \left(\frac{E_B-E_A}{N_B-N_A}\right) \end{equation*}

 

Exemplo de Aplicação e Cálculo com coordenadas UTM

Considere dois pontos com as seguintes coordenadas (E,N) no sistema de projeção UTM, fuso 24S:

Ponto A: E = 791.933,195m, N = 9.279.836,409m

Ponto B: E = 791.938,441m, N = 9.279.783,172m

 

Cálculo da Distância

Substituindo esses valores na fórmula do cálculo de distância (d), obtemos o azimute de A para B.

    \[\begin{gathered} d=\sqrt{\Delta E^2+\Delta N^2} \\ \Delta E=E_B-E_A=791.938,441 \mathrm{~m}-791.933,195 \mathrm{~m}=5,246 \mathrm{~m} \\ \Delta N=N_B-N_A=9.279 .783,172 \mathrm{~m}-9.279 .836,409 \mathrm{~m}=-53,237 \mathrm{~m} \\ d=\sqrt{(5,246 \mathrm{~m})^2+(-53,237 \mathrm{~m})^2} \\ d=\sqrt{27,494 \mathrm{~m}^2+2.834,007 \mathrm{~m}^2} \\ d \approx \sqrt{2.861,501 \mathrm{~m}^2} \approx 53,502 \mathrm{~m} \end{gathered}\]

Cálculo do Azimute

Substituindo esses valores na fórmula de azimute, obtemos o azimute de A para B.

Azimute (A z) de A para B:

    \[\begin{gathered} A z=\arctan \left(\frac{E_B-E_A}{N_B-N_A}\right) \\ A z=\arctan \left(\frac{791.938,441 \mathrm{~m}-791.933,195 \mathrm{~m}}{9.279 .783,172 \mathrm{~m}-9.279 .836,409 \mathrm{~m}}\right) \\ A z=\arctan \left(\frac{5,246 \mathrm{~m}}{-53,237 \mathrm{~m}}\right) \\ A z \approx \arctan (-0,0987) \approx174,37^{\circ} \end{gathered}\]

 

Como obter a Distância e Azimute no QGIS

No QGIS, um software de Sistema de Informação Geográfica (SIG), você pode medir distâncias e azimutes usando a ferramenta de medição integrada. Para realizar essa tarefa:

  1. Abra o QGIS e carregue o mapa onde você deseja medir as distâncias e os azimutes.
  2. Selecione a camada ou adicione os pontos:
    • Certifique-se de ter a camada correta carregada ou adicione os pontos no mapa.
  3. Configure a Aderência (snapping) para clicar exatamente no vértice.
  4. Ative a ferramenta de medição:
    • No menu superior, vá para “Visualizar” ou “View”.
    • Selecione “Barra de Ferramentas” ou “Toolbars”.
    • Certifique-se de que a barra de ferramentas “Medição” ou “Measure” esteja ativada. Se não estiver, marque a opção para ativá-la.
  5. Use a ferramenta de medição:
    • Clique no ícone da ferramenta de medição na barra de ferramentas (geralmente, é um ícone de régua ou uma fita métrica).
    • Selecione o tipo de medição desejado (distância ou azimute).
    • Clique nos pontos do mapa que você deseja medir.
  6. Para medir distância:
    • Clique no primeiro ponto e, em seguida, no segundo ponto.
    • A distância será exibida na unidade configurada no QGIS (cartesiana ou elipsoide).
  7. Para medir azimute:
    • O azimute pode ser exibido como parte das informações de medição, dependendo da versão do QGIS. você pode ver o azimute na janela de informações da medição.

Passo a passo para medir distâncias e azimutes no QGIS!

 

Funções para calcular Distâncias e Azimutes com Python

 

Função para cálculo da distância

A função calcular_distancia pode ser usada para calcular a distância entre quaisquer pontos no plano cartesiano representados por coordenadas (E, N).

from numpy import sqrt

def calcular_distancia(A, B):
    # Cálculo da distância euclidiana entre dois pontos
    delta_x = B[0] - A[0]
    delta_y = B[1] - A[1]

    distancia = sqrt(delta_x ** 2 + delta_y ** 2)
    return distancia

# Exemplo de Uso:
A = (791933.195, 9279836.409)
B = (791938.441, 9279783.172)
distancia_AB = calcular_distancia(A, B)
print("Distância entre A e B:", distancia_AB)

 

Função para cálculo do Azimute

A função calcular_azimute calcula os azimutes AB e BA (contra-azimute). Esta função lida com todos os casos dos quadrantes e garante que os ângulos estejam dentro do intervalo desejado (0° a 360°).

from numpy import arctan2, pi, degrees
def calcular_azimute(A, B):
    # Cálculo dos Azimutes entre dois pontos (Vetor AB origem A extremidade B)
    delta_x = B[0] - A[0]
    delta_y = B[1] - A[1]
    AzAB = arctan2(delta_x, delta_y)
    AzBA = AzAB + pi if AzAB < 0 else AzAB - pi
    return (AzAB % (2 * pi), AzBA % (2 * pi))
# Exemplo de uso:
A = (791933.195, 9279836.409) 
B = (791938.441, 9279783.172)
resultado = calcular_azimute(A, B)
print("Azimute AB:", degrees(resultado[0]))
print("Azimute BA:", degrees(resultado[1]))

 

Observações Importantes

  • Os azimutes e distâncias são obtidos com coordenadas projetadas no sistema UTM, sendo referenciados ao norte da projeção, não ao norte geográfico verdadeiro.
  • Devido à projeção cartográfica, as distâncias calculadas com coordenadas UTM sofrem pequenas distorções. Essas distorções podem ser corrigidas dividindo as distâncias pelo fator kappa, que varia com a localização.
  • Uma alternativa para obter azimutes verdadeiros e distâncias mais próximas da realidade no terreno é trabalhar com coordenadas no Sistema Geodésico Local (SGL), como adotado pelo INCRA.

Conclusão

Conhecer e calcular azimutes e distâncias é essencial para profissionais que atuam na área de topografia. As fórmulas e algoritmos apresentados neste artigo fornecem as ferramentas necessárias para realizar medições precisas em campo, levando em consideração as particularidades do sistema UTM e as correções necessárias para garantir a precisão das informações obtidas. Compreender esses conceitos é fundamental para garantir a qualidade dos dados topográficos e o sucesso de projetos que dependem dessas informações.

 

Curso de Automatização no QGIS

Você é um profissional da área de topografia, cartografia, engenharia ou geodésia? Deseja aprimorar suas habilidades e automatizar o processo de geração de plantas topográficas e memoriais descritivos? Este curso é a solução que você estava esperando!

Aprenda a usar o software QGIS para gerar plantas topográficas detalhadas e memoriais descritivos precisos, incorporando azimutes e distâncias em suas medições.

Não perca a oportunidade de dominar a automatização no QGIS e se destacar em sua área de atuação. Junte-se a nós e inicie sua jornada de aprendizado e crescimento profissional!

CLIQUE AQUI

Compartilhes nas redes Sociais

ÚLTIMOS POSTS
CONHEÇA NOSSOS CURSOS
Curso drone
Python para QGIS
Sensoriamento Remoto com QGIS
Leandro França

Politica de Privacidade

FALE CONOSCO
contato@geoone.com.br

Instagram Youtube